(4) Queue 와 Stack

List로 구현되어 자료의 순서가 중요할 때 사용하는, Queue와 Stack

1. Queue (큐)

(1) 큐의 시간복잡도

doubly linked list로 구현하여, enqueue(0), enqueue(n) / dequeue(0), dequeue(n) 의 시간 복잡도가 모두 O(1)입니다.

(2) 큐를 사용하는 경우

1. FIFO (선입선출) 상황
2. BFS 경우

큐 자료구조가 단독으로 나오는 경우는 거의 없으며, BFS 알고리즘에서 같이 나옵니다.

---

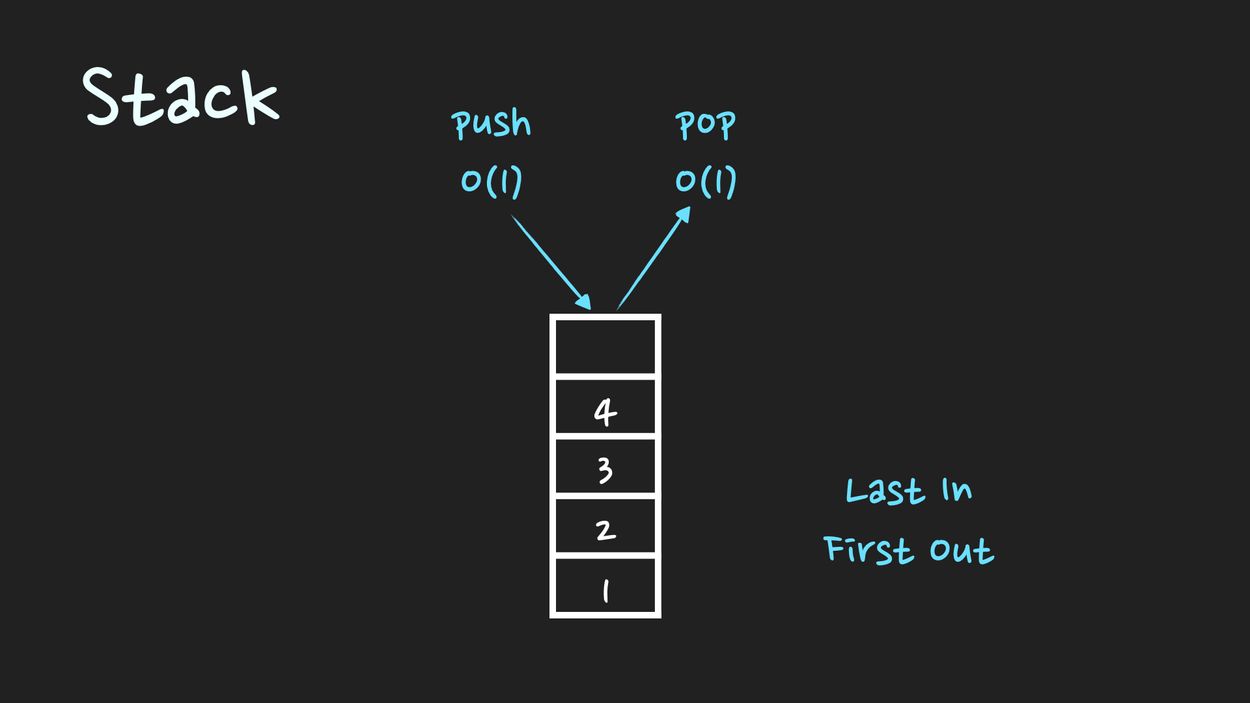
2. Stack (스택)

(1) 스택의 시간복잡도

array list로 구현하여, last에서의 pop과 push만 시간 복잡도 O(1)입니다.

(2) 스택을 사용하는 경우

1. LIFO (후입선출)
2. DFS 경우

앞에 소제목에서 말했듯이, 순서가 중요하고 특정 조건하에서 반응(pop, push)하는 상황에서 사용할 수 있습니다.

🍓 valid-parenthesis (괄호 유효성) 문제

특정 조건하에서만 pop과 push가 일어남.

# 문제 상황 : {},(),[] 세 가지의 괄호 유효성 검사. True or False 출력  
# 입력제한 : 1 <= s.length <= 10^4
# 시간복잡도 : O(n)

class Solution:
    def isValid(self, s: str) -> bool:
        open = ['(', '[', '{']
        close = [')', ']', '}']
        if len(s)%2 == 1:
            return False
        if s[0] in close:
            return False
        
        new = []
        for i in range(1,len(s)+1):
            char = s[-i]
            if char in close:
                new.append(char)
            else:
                idx = open.index(char)
                if new == []: return False
                if idx != close.index(new.pop()): return False
        if new != []:
            return False
        else: 
            return True

🍓 daily-temperature 문제

특정 조건하에서만 pop과 push가 일어남 + 인접하지 않은 idx에도 영향을 줌

# 문제 상황 : 연속한 날짜의 각 온도를 input 배열로 받아, 해당 날짜에서 따뜻해지려면 몇 일이 걸리는지 answer 배열 return. 만약, 따뜻해지는 날이 없는 경우 0   
# 입력제한 : 1 <= temperatures.length <= 10^5
# 시간복잡도 : O(n)

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        stack = []
        answer = [0 for _ in range(len(temperatures))]
        for i, n in enumerate(temperatures):
            while stack and stack[-1][0] < n:
                _, idx = stack.pop()
                answer[idx] = i - idx
            stack.append((n, i))

        return answer

# 접근 방법 : 문제의 단순화를 통해, 증가 감소의 경우로 나누는 접근 방법 떠올리기!        

다음에는 Hash Table 에 대해서 포스팅 하겠습니다 :)

해당 시리즈의 포스트는 인프런에서 제공하는 개발남노씨의 코딩테스트 강의 를 바탕으로 작성하였습니다.