(5) Hash Table과 시간복잡도

April 6, 2023

⭐ Hash table의 핵심은 "key in dic"의 시간 복잡도가 O(1) 이라는 것 입니다.

- key-value 쌍이 필요할 때보다 빠르게 있는지 탐색할 때, 매우 빈출!

- 메모리를 사용하여, 시간복잡도를 줄인다!

- if key in dic, while key in dic

(1) Hash table 내부

해시테이블 내부

Hash table은 (1) Array list 혹은 (2) Array list + Linked list 로 구현되는데,
파이썬에서 Dictionary는 (1) Array list based 로 구현된 Hash Table을 말합니다.

(1) Array list based 와 (2) Array list + Linked list base 차이는 Hash Table의 collision 문제에 대한 해결 방법인 Open addressing / Seperate Chaining 다르다는 것입니다.

(2) 시간 복잡도

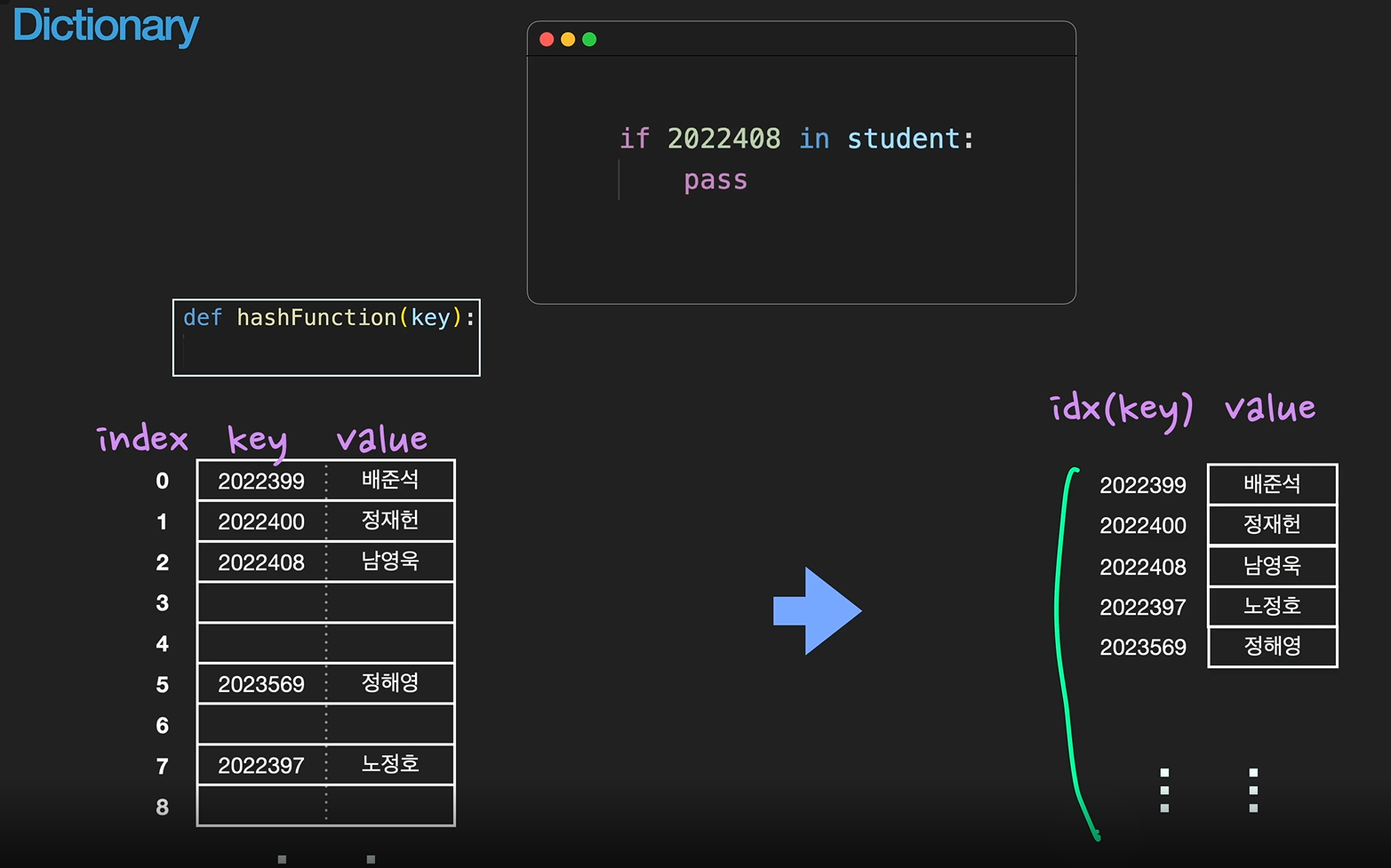
해시테이블 KeyIn

해시 테이블은 hashFunction()에 의해서 구현되는데, hashFunction()에 key값을 넣으면, key%9 을 idx로 return 하는 방식입니다.
하지만, 우리는 내부 원리를 빼고 key를 idx로 두고 단순하게 생각해도 됩니다.

시간 복잡도는 저장, 삭제, 검색 모두 O(1) 입니다.
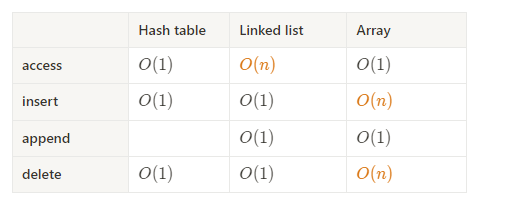
해시테이블 시간복잡도

(3) 사용하는 경우

key in dic 의 시간복잡도가 O(1)

리스트에서, num in list 의 시간 복잡도는 O(n) 이다.
따라서, 특정 원소가 있는지 찾고 싶을 때 (기억하고 싶을 때) 딕셔너리를 쓰면 된다!

🍓 twoSum 문제

(1) 문제 상황 : 입력배열의 2개의 숫자를 더해서 target값이 될 수 있는 경우가 있다면 False 출력
(2) 오류 파악 : 중복하면 안된다.
(3) 입력제한 : 0 < len(nums) <= 10^4
(4) 시간복잡도 : O(nlogn)

예를들어, 다음과 같은 리스트의 숫자 중 2개를 뽑아 6이 되도록 하는 문제를 풀어봅시다.
[1, 12, 3, 5, 2]

(a) 완전탐색 (brute-force)

O(n^2)이 걸립니다.

(b) sort & list

sort 함수는 시간 복잡도가 O(logn)입니다.
sort 함수를 통해, [1, 2, 3, 5, 12] 로 정렬이 됩니다. 맨 앞과 맨 뒤에서 더하면서 target 값이 6을 찾아 나갈 수 있습니다.

예를들어, 1+12=13에서 target값 보다 크니 뒤포인터를 하나 앞으로 땡겨
1+5=6 찾았습니다.

(c) Hash talbe

해시테이블을 사용하면 key in dic 로 시간복잡도는 O(n)입니다.

    def twoSum_dic(self, nums, target):
        dic = {}
        for i, v in enumerate(nums):
            dic[v] = i
        
        for i, v in enumerate(nums):
            needed_num = target - v
            if needed_num in dic:       # BigO(1)
                if i == dic[needed_num]: continue
                else:
                    return [i, dic[needed_num]]
        return False        

🍓 Longest Consecutive Sequence 문제

(1) Hash table로 풀기

시간복잡도는 n + n = BigO(n) 입니다. worst case의 경우 n^2이 될 수 있으므로, 시작점에서만 while문 돌도록 if문 추가합니다.
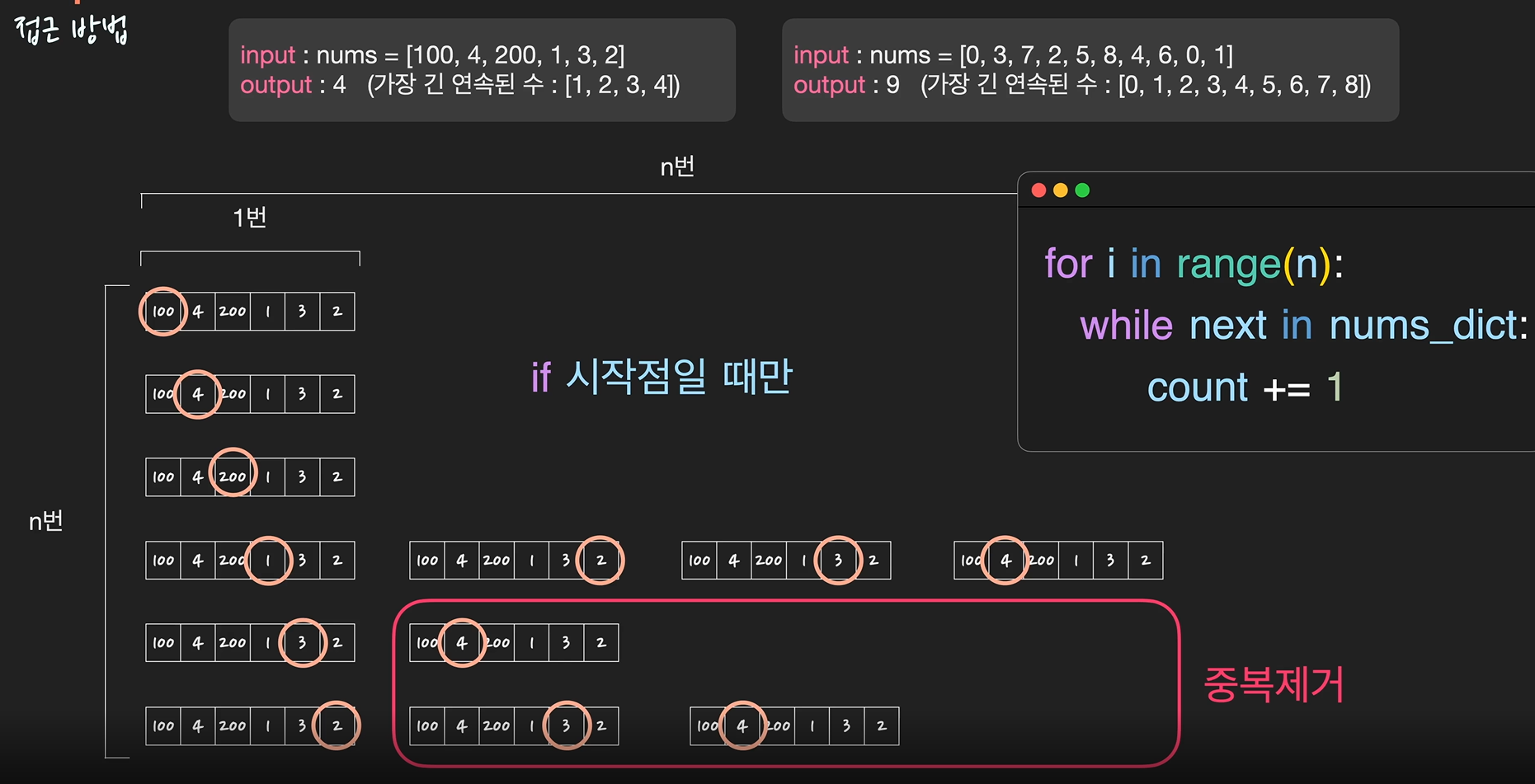
문제 접근방법

[Hash table로 푸는 경우, 코드 접기/펼치기]

class Solution:
    def longestConsecutive(self, nums: list) -> int:
        longest = 0
        num_dic = {}
        for v in nums:
            num_dic[v] = True
        
        for v in nums:
            prev = v-1
            next = v+1
            if prev not in num_dic:
                count = 1
                while next in num_dic:
                    count += 1
                    next += 1
                longest = max(longest, count)
        return longest    

(2) Hash set으로 풀기

Hash set은 Hash table과 마찬가지로 hashfunction()에 의해 작동하므로, 원리와 시간 복잡도가 같습니다.

[set으로 푸는 경우, 코드 접기/펼치기]

class Solution(object):
    def longestConsecutive(self, nums):
        longest=1
        num_set = set(nums)
        for x in num_set:
            target=x+1
            val=1
            while target in num_set:
                target += 1
                val += 1
            longest = max(longest, cnt)
        return longest

다음에는 Tree에 대해서 포스팅 하겠습니다 :)

해당 시리즈의 포스트는 인프런에서 제공하는 개발남노씨의 코딩테스트 강의 를 바탕으로 작성하였습니다.