(11) Graph 심화
그래프 문제에서 사용할 수 있는 4가지 알고리즘에 대해서 알아보겠습니다.
(모두 인접행렬보다 인접리스트(혹은 딕셔너리)로 만들어야 효율이 높다.)
Dijkstra, Bellman-Ford, Floyd-Warshall, Kruskal 의 대표적인 문제와 템플릿 코드를 소개합니다.
다익스트라와 벨먼포드는 최단경로를 구하는 문제입니다.
벨먼포드는 간선이 음수일 때도 고려한 알고리즘 이고, 다익스트라는 간선이 양수인 특수한 경우에 최적의 해를 찾는 알고리즘입니다.
다익스트라와 벨먼포드는 특정 노드에서 다른 모든 노드의 최단 경로를 찾는 문제라면,
플로이드 와샬은 모든 노드에서 다른 모든 노드의 최단 경로를 찾는 문제입니다.
(즉, 모든 정점 쌍의 최단 경로를 찾는 문제)
크루스칼은 최소 스패닝 트리(Minimum Spanning Tree, MST)를 찾는 문제입니다.
최소 스패닝 트리는 그래프의 모든 정점을 연결하는 가장 경제적인 방법을 찾는 데 사용됩니다.
그러면, 하나씩 살펴봅시다.
1. 다익스트라: 양수 간선의 최단경로
가중치가 없는 그래프의 최단 경로는 BFS로 풀고, 가중치 그래프에서 최단경로를 구할 때는 다익스트라를 쓴다.
우선순위 큐를 사용하여 효율적으로 작동한다.
import heapq
def dijkstra(graph, start):
distances = {node: float('infinity') for node in graph}
distances[start] = 0
priority_queue = [(0, start)]
while priority_queue:
current_distance, current_node = heapq.heappop(priority_queue)
if distances[current_node] < current_distance:
continue
for adjacent, weight in graph[current_node].items():
distance = current_distance + weight
if distance < distances[adjacent]:
distances[adjacent] = distance
heapq.heappush(priority_queue, (distance, adjacent))
return distances
크루스칼 알고리즘의 시간 복잡도
우선순위큐에서 가장 짧은 간선을 꺼내는 작업 O(logE)를 최악의 경우 E번
따라서, 시간복잡도는 O(ElogE)이다.
[ 관련 문제 : Dijkstra: Shortest Reach 2]
-
길이 없는 노드는 inf 값이 아닌 -1을 출력해야 한다.
-
graph는 heapq 때문에 (e,v)로 들어가지만, dists는 (v, 누적e) 헷갈릴 수 있다. 주의!
def shortestReach(n, edges, s):
# Write your code here
graph = {key:[] for key in range(1, n+1)}
for a, b, e in edges:
graph[a].append((e,b))
graph[b].append((e,a))
if not graph[s]:
return [-1]*(n-1)
dists = {node: -1 for node in graph}
hque = [(0,s)]
while hque:
dist, node = heappop(hque)
if dists[node] != -1 and dist > dists[node]:
continue
for e, next_node in graph[node]:
next_dist = dist + e
if dists[next_node] == -1 or next_dist < dists[next_node]:
dists[next_node] = next_dist
heappush(hque, (next_dist, next_node))
del dists[s]
ans = [value for key, value in sorted(dists.items(), key=lambda x:x[0])]
return ans
2. 벨만-포드: 정수 간선의 최단경로
def bellman_ford(graph, start):
distances = {node: float('infinity') for node in graph}
distances[start] = 0
for _ in range(len(graph) - 1):
for node in graph:
for adjacent, weight in graph[node].items():
if distances[node] + weight < distances[adjacent]:
distances[adjacent] = distances[node] + weight
# Check for negative weight cycles : 더 줄일 수 가 있다면, 음수 가중치
for node in graph:
for adjacent, weight in graph[node].items():
if distances[node] + weight < distances[adjacent]:
print("Graph contains a negative weight cycle")
return None
return distances
벨만-포드는 이름만 어렵지 음수 간선을 고려하기 위해서 n-1번 반복해서 인접 노드와의 간선을 업데이트하는 것일 뿐이다.
첫번째 삼중 for문에서 이를 수행한다.
추가로, 음수 가중치에 cycle이 있는 경우 값이 음수의 무한대로 발산할 수 있다.
두번째 이중 for문에서 음수 가중치가 포함된 cycle이 있는지 확인한다.
벨만-포드 시간복잡도
모든 정점에 대해 모든 간선을 검사하고, 이 과정을 V−1 번 반복하므로 시간 복잡도는 O(VE)이다.
[ 관련 문제 : 11657번 타임머신]
- 무방향이 아니였다. 방향 그래프 문제이다.
from sys import stdin
input = stdin.readline
n, m = map(int, input().split())
graph = {node: [] for node in range(1, n+1)}
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((c,b))
distances = {node: float('inf') for node in graph}
distances[1] = 0
for _ in range(n-1):
for node in range(1, n+1):
for edge, adjacent in graph[node]:
if distances[node] + edge < distances[adjacent]:
distances[adjacent] = distances[node] + edge
for node in range(1, n+1):
for edge, adjacent in graph[node]:
# 더 줄일 수 가 있다면, 음수 가중치
if distances[node] + edge < distances[adjacent]:
print(-1)
exit(0)
del distances[1]
ans = [dist if dist != float('inf') else -1 for _, dist in distances.items()]
print(*ans)
3. 플로이드-와샬: 모든 정점 쌍의 최단경로
경로의 중간노드를 for문으로 돌면서 최적의 경로를 update하는 DP 문제이다.
def floyd_warshall(graph):
distances = {node: {other_node: float('infinity') for other_node in graph} for node in graph}
for node in graph:
distances[node][node] = 0
for adjacent, weight in graph[node].items():
distances[node][adjacent] = weight
for k in graph:
for i in graph:
for j in graph:
distances[i][j] = min(distances[i][j], distances[i][k] + distances[k][j])
return distances
플로이드와샬 시간복잡도
세 개의 중첩된 루프를 사용하여 모든 정점 쌍에 대해 최단 경로를 계산합니다. 따라서 시간 복잡도는 O(V**3)이다.
[ 관련 문제 : Floyd - City of Blinding Lights]
4. 크루스칼: MST 찾기
간선을 정렬한 후 유니온 파인드를 사용하여 MST를 구하는 문제이다.
def find(parent, node):
if parent[node] != node:
parent[node] = find(parent, parent[node]) # return find(parent, parent[node] 에서 "path compression"
return parent[node]
def union(parent, rank, node1, node2):
root1 = find(parent, node1)
root2 = find(parent, node2)
if rank[root1] < rank[root2]:
parent[root1] = root2
elif rank[root1] > rank[root2]:
parent[root2] = root1
else:
parent[root1] = root2
rank[root2] += 1
def kruskal(graph, vertices):
parent = {node: node for node in vertices}
rank = {node: 0 for node in vertices}
mst = []
edges = sorted(graph, key=lambda x: x[2])
for edge in edges:
node1, node2, weight = edge
# 두 노드가 서로 다른 집합에 속해 있다면, 해당 간선을 MST에 추가하고 합친다.
if find(parent, node1) != find(parent, node2):
mst.append(edge)
union(parent, rank, node1, node2)
# 같은 집합이라면, 사이클이 형성되기 때문에 해당 간선을 무시한다.
return mst
-
Path compression(경로 압축)

-
rank
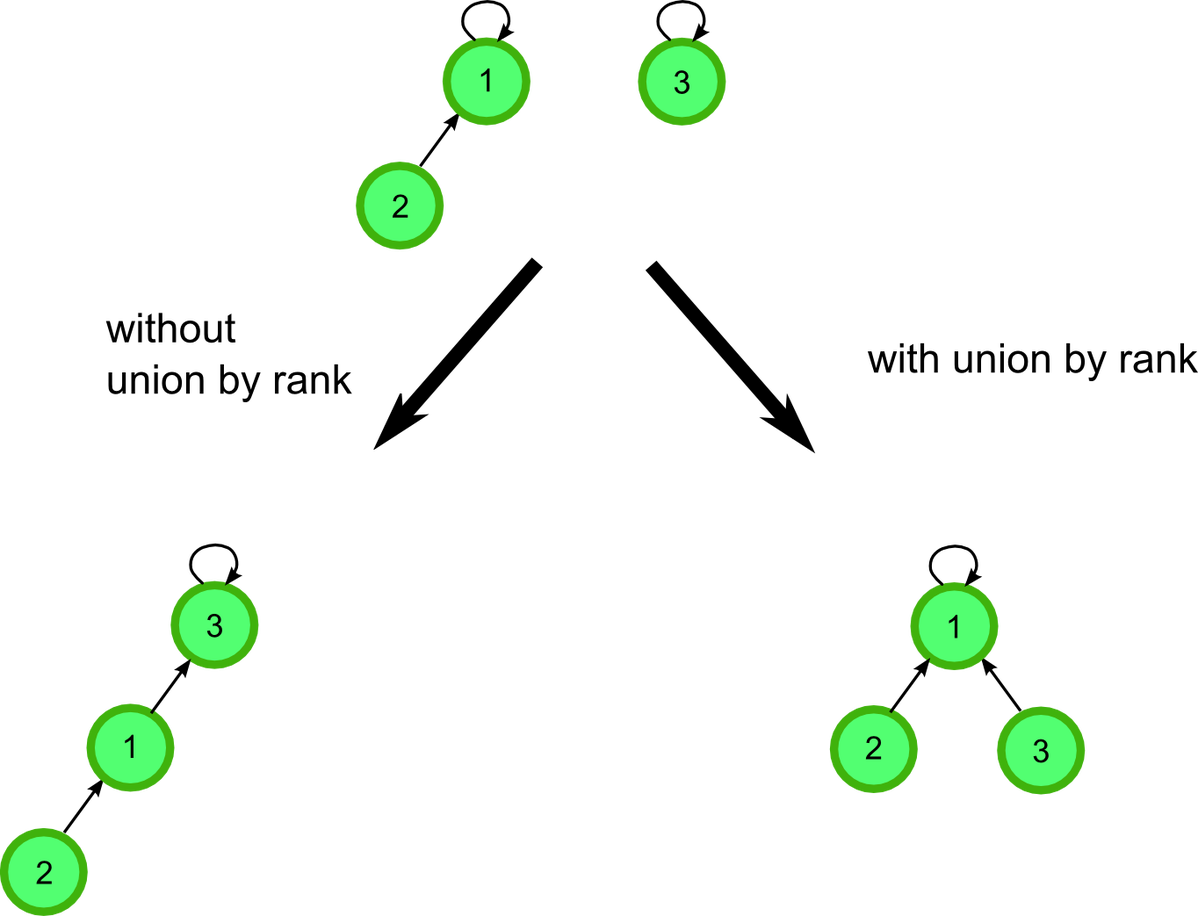
트리의 깊이 유니온 파인드 연산 실행시간에 영향을 주는데 트리를 합칠 때 높이가 작은 트리를 높이가 큰 트리의 루트에 붙이면 높이가 높아지지 않는다.
이렇게 유니온 바이 랭크(union by rank)는 높이가 작은 트리를 큰 트리의 루트에 붙이는 방법이다.
※ 단, 높이가 같은 트리를 합칠 땐 높이가 +1 높아진다.
우리는 여기서 랭크라는 표현을 쓰는데, 트리의 높이는 위에서 살펴본 path compresstion에 의해서 줄어들 수 있고 업데이트 되지 않기 때문이다. 그래서 랭크라는 표현을 쓴다.
크루스칼의 시간복잡도
간선을 가중치에 따라 정렬하는 데 O(ElogE) 시간이 걸리며,
E개의 간선에 대해 유니온-파인드 연산을 수행하는 데 O(ElogV) 시간이 걸린다.
간선의 수가 정점의 수보다 많지 않다면 (E≤V**2), O(logE)=O(logV)이므로 시간 복잡도는 O(ElogV)가 된다.

Leave a comment