(7) Graph

April 10, 2023

Graph는 tree보다 더 큰 개념으로 정점(vertex)들의 집합 V와 이를 연결하는 간선(edges)들의 집합 E로 구성된 자료구조입니다.

Graph는 트리와 달리 방문 표시를 해야합니다. BFS와 DFS 모두.

시간복잡도는 완전탐색이니까 O(n)인데, 사실 O(n+E) 입니다.

모든 정점에 한 번만 방문한다고 해도, 간선만큼 갈 지 말지 결정해야 하기 때문입니다.

다만, 최단거리 문제는 BFS로 풀 때 모두 탐색하기 전에 끝날 수 있습니다. 따라서, 최단거리 문제는 BFS로 풀어야 효율적입니다.

현실세계의 연결관계를 그래프로 표현

그래프 활용

(1) Graph 종류

코테에 나오는 그래프는 정해져 있습니다!

방향 그래프 vs 무향 그래프
다중 그래프 vs 단순 그래프 (두 정점의 간선은 하나)
가중치 그래프 => 다익스트라

(2) Graph 표현 방법

그래프는 3가지로 표현 할 수 있습니다.

1. 인접 리스트 (adjacency list) ⭐

그래프를 가장 효율적으로 표현할 수 있는 방법이기 때문에, 가장 많이 쓰입니다.
보통 그래프는 정점의 수에 비해 간선이 적기 때문이죠!

2. 인접 행렬 (adjacency matrix)

정점의 개수만큼 2차원 배열을 만들어서 표현하는 방법입니다.

3. 암시적 행렬 (implicit graph) ⭐

(0,0)~(n-1,n-1)까지의 경로, 도형면적 구하기 문제 등
Binary matrix이지만, 위아래양옆 방향으로 간선이 연결되어있는 graph로 볼 수 있습니다.
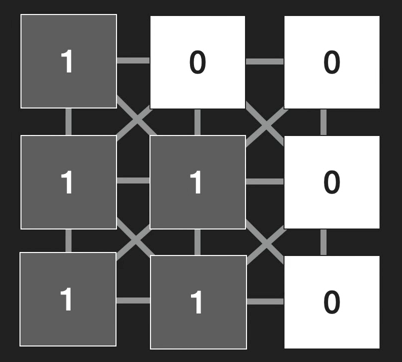
암시적 그래프
그래프 문제에서 가장 많이 나오는 문제입니다.

(3) BFS

BFS는 물수제비 현상이라고 생각하면 쉽습니다.
BFS와 DFS 모두 Graph의 정점을 완전탐색하는 방법이므로, BFS로 풀어도 되고 DFS로 풀어도 됩니다.

하지만, BFS는 물수제비처럼 가까운 것부터 차례로 탐색하므로 최단거리 문제에서는 BFS로 푸는 것이 효율적입니다.
DFS는 모든 경우의 수를 다 시도해야 알 수 있기 때문입니다.

BFS

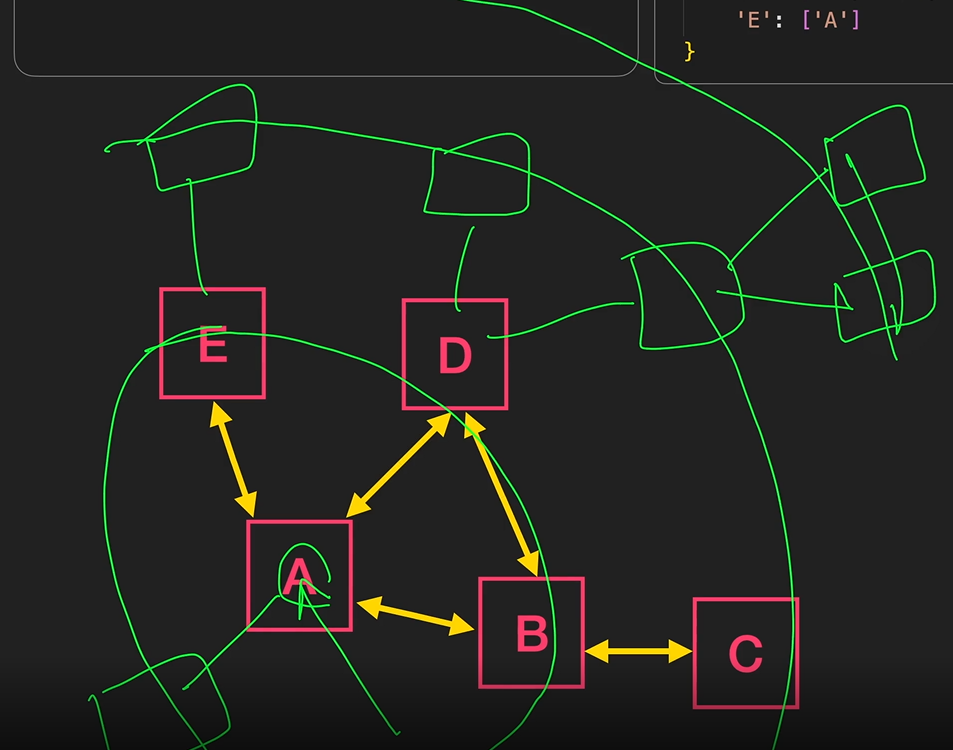
그래프 BFS의 템플릿 ⭐

from collections import deque
# 그래프, 인접 리스트로 표현
graph = {
    'A' : ['B', 'D', 'E'],
    'B' : ['A', 'C', 'D'],
    'C' : ['B'],
    'D' : ['A', 'B'],
    'E' : ['A']
}

def bfs(graph, start_v):
    q = deque(start_v)
    visited = [start_v]
    while q:
        cur_v = q.popleft()
        for nex_v in graph[cur_v]:
            if nex_v not in visited:
                q.append(nex_v)
                visited.append(nex_v)   # 무한루프에 빠질 수 있으므로, 방문예약 시 visited 해야함.

    return visited

print(bfs(graph, 'A'))  # ['A', 'B', 'D', 'E', 'C']

(4) DFS

DFS는 루트 정점의 연결 정점을 subgraph의 새로운 루트 정점으로 보고, 재귀로 문제를 쪼개서 생각합니다.

그래프 DFS의 템플릿 ⭐

from collections import deque
graph = { ... }
visited = []

def dfs(root):
    visited.append(root)
    for v in graph[root]:
        if v not in visited:
            dfs(v)
dfs('A')
print(visited)  #['A', 'B', 'C', 'D', 'E']

(5) 그래프를 사용하는 경우

Graph 구현
BFS 너비 우선 탐색
DFS 깊이 우선 탐색

🍓 Number of Islands 문제

제한 사항 : 1 <= grid.length, grid[i].length <= 300
접근 방법 : 섬은 색칠, 새로운 섬 발견? 또 색칠
BFS
시간 복잡도 : 순회 O(n) (대략 10^5)

from collections import deque 
class Solution(object):
    def numIslands(self, grid):
        m = len(grid) 
        n = len(grid[0])
        dx = [0,0,1,-1]
        dy = [1,-1,0,0]
        islandsN = 0 
        
        # 여기에 정의하면 함수의 파라미터를 새로 메모리에 올리지 않아도 됨.
        def bfs(x,y):
            q = deque()                 # 튜플은 초기화 시 넣을 수 없음.
            grid[y][x] = '0'
            q.append((x,y))
            while q:
                cur_x, cur_y = q.popleft()
                for i in range(4):
                    nxt_x = cur_x + dx[i]
                    nxt_y = cur_y + dy[i]
                    if nxt_x < 0 or nxt_x >= n or nxt_y < 0 or nxt_y >= m:
                        continue
                    if grid[nxt_y][nxt_x] =='1':
                        grid[nxt_y][nxt_x] = '0'
                        q.append((nxt_x, nxt_y))
            
        for x in range(n):
            for y in range(m):
                if grid[y][x] == '1':
                    islandsN += 1
                    bfs(x,y)
                    # dfs()     
                           
        return islandsN
    
sol = Solution()
print(sol.numIslands([["1","1","0","0","0"],["1","1","0","0","0"],["0","0","1","0","0"],["0","0","0","1","1"]]))

🍓 Shortest Path 문제

최단경로 문제는 BFS가 효율적 입니다. DFS로도 풀 수 있지만, 모든 경우의 수를 해봐야합니다.

제한 사항 : 1 <= grid.length, grid[i].length <= 100
접근 방법 : 최단경로 문제는? 무조건 BFS. 먼저 도착한 게 최단거리이므로, shortest 저장할 필요 없음!
BFS
시간 복잡도 : 순회 O(n)

from collections import deque
class Solution(object):
    def shortestPathBinaryMatrix(self, grid):
        n = len(grid)
        if grid[0][0] == 1 or grid[n-1][n-1] == 1:
            return -1 
        if n == 1:
            return 1
        
        # shortest = [[10001]*n for _ in range(n)]  # BFS 먼저 도착한 게 최단거리임. shortest 필요 없음.
        dx = [0,0,1,-1,1,1,-1,-1]
        dy = [1,-1,0,0,1,-1,1,-1]
        q = deque()
        grid[0][0] = 1                              # 방문 처리
        q.append((0,0,1))
        
        while q:
            x, y, dist = q.popleft()
            for i in range(8):                      # 방문 예약
                next_x = x + dx[i]
                next_y = y + dy[i]
                if next_x < 0 or next_x >= n or next_y < 0 or next_y >= n:
                    continue
                if grid[next_y][next_x] == 1:
                    continue
                if next_x == n-1 and next_y == n-1:
                    return dist + 1
                else:
                    grid[next_y][next_x] = 1
                    q.append((next_x, next_y, dist+1))
        
        return -1
        

sol = Solution()
print(sol.shortestPathBinaryMatrix([[0,0,0],[1,1,0],[1,1,0]]))

🍓 keys and rooms 문제 ⭐

제한 사항 : 2 <= rooms.length <= 1000, 1 <= sum(rooms[i].length) <= 3000
시간 복잡도 : O(V+E) = O(4000)

BFS로 풀면 ?

from collections import deque
class Solution:
  def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
      n = len(rooms)
      visited = [False]*n
      q = deque()
      visited[0] = True
      q.append(0)
      while q:
          v = q.popleft()
          for next_v in rooms[v]:     # keys를 추가하지 않아도 됨
              if not visited[next_v]:
                  visited[next_v] = True
                  q.append(next_v)
        
      if all(visited) :
          return True
      else:
          return False

DFS로 풀면 ?

class Solution:
    def canVisitAllRooms(self, rooms) -> bool:
        n = len(rooms)
        visited = [False]*n

        def dfs(v):
            visited[v] = True
            for next_v in rooms[v]:      # keys를 추가하지 않아도 됨
                if not visited[nex_v]:
                    dfs(next_v)
         
        dfs(0) 

        if all(visited):
            return True
        else:
            return False

sol = Solution()
sol.canVisitAllRooms([[1],[2],[3],[]])

BFS, DFS의 시간복잡도는 O(n) 입니다.

다음에는 많이 사용되는 알고리즘 DP에 대해서 포스팅 하겠습니다 :)

해당 시리즈의 포스트는 인프런에서 제공하는 개발남노씨의 코딩테스트 강의 를 바탕으로 작성하였습니다.