소수 판별 (O(n), O(root(n)), O(nlogn))

소수(PrimeNumber)를 판별하는 방법(알고리즘) 3가지를 소개하겠습니다.

소수란 1과 자신만을 약수로 가지는 자연수로, 1은 제외됩니다.

소수를 판별하는 방법은 (1) 브루트포스 방법, (2) 브루트포스에서 약수의 대칭성을 이용한 방법, (3) 에라토스테네스의 체 입니다.

1. 브루트포스 방법

일종의 브루트포스 방식으로, 판별하고자 하는 숫자 N을 N-1 숫자까지 나누어 떨어지는 경우가 있는지 확인하는 것입니다.

시간복잡도는 O(N) 으로 구현이 간단하지만 시간효율성이 떨어지는 방법입니다.

def isPrime(n):
    for i in range(2,n):
        if n % i == 0 :
            return False    # 합성수로 판별
    return True             # 소수로 판별

2. 브루트포스 + 약수의 대칭성 이용

약수의 대칭성으로 인해, N = A * B (A>=B) 에서 대칭을 기준으로 반만 고려하면 됩니다.

그러면, A만 고려한다고 했을 때, 가능한 A의 최댓값은 root(N) (포함) 입니다.

100을 예로 들겠습니다. < 2, 4, 5, 10, 20, 25, 50 > 이 경우 10까지만 고려해보면 됩니다.

따라서, 시간복잡도는 O(root(N)) 입니다.

더 자세한 설명 참고 블로그

import math

def isPrime(n):
    for i in range(2,int(math.sqrt(n))+1):
        if n % i == 0:
            return False
    return True

3. 에리토스테네스의 채

대량의 소수를 한꺼번에 판별 할 때 사용하는 방법입니다.

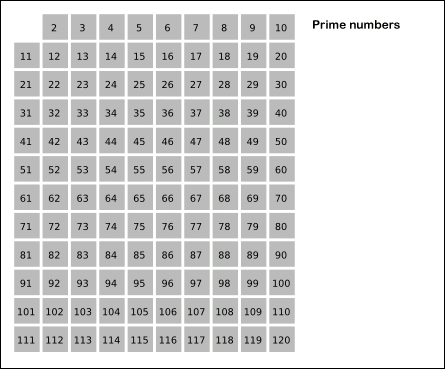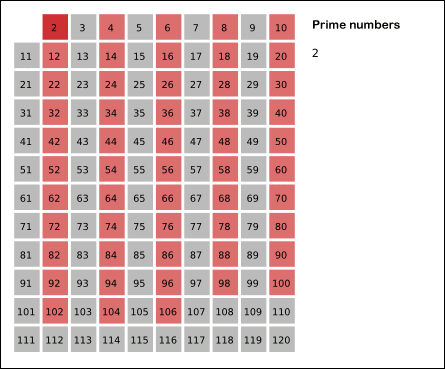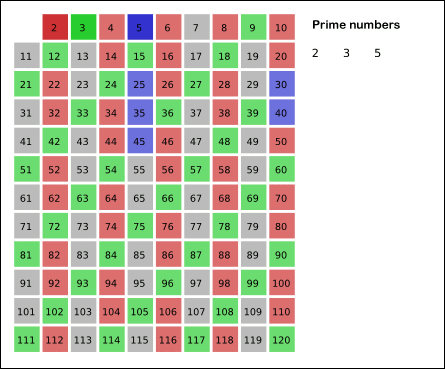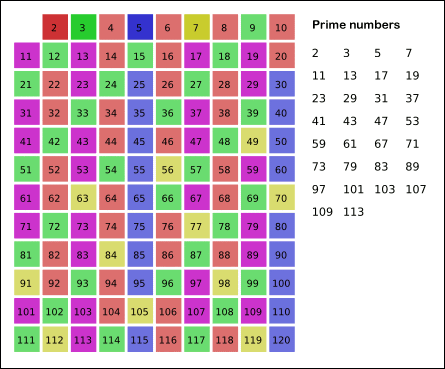
시간복잡도는 O(NlogN)으로 거의 선형시간에 작동하는 효율적인 방법입니다.

import math
N = 25
eritos = set(range(2,N+1))          # 에라토스테네스 체 채우기

for i in range(2, int(math.sqrt(N))+1): # 에라토스테네스 체 빼기
    eritos -= set(range(i*2,N+1,i))

eritos  # {2, 3, 5, 7, 11, 13, 17, 19, 23}

---

코테 문제

(1) k진수에서 소수 개수 구하기 (lv2)

• 문제 상황 : n을 k진법으로 바꾸고, 0을 기준으로 split 한 후, 10진법 기준으로 소수의 개수를 찾기

• k진법으로 변환

• 소수 찾기

import math
import re 

def solution(n, k):
    answer = 0
    
    convert = ''
    while n > 0:            # 시간복잡도 O(13)
        n, r = divmod(n,k)
        convert += str(r)
    convert = convert[::-1]    
    convert = re.findall('[^0]+', convert)
    
    def isPrime(a):
        for i in range(2,int(math.sqrt(a))+1):    
            if a % i == 0:
                return False        
        return True
    
    for v in convert:       # O(N*root(N))
        v = int(v)
        if v != 1 and isPrime(v):
            answer += 1
    
    return answer

(2) 소수 찾기 (lv2)

• map 함수 : map(함수, 적용할 자료형)

• join 함수 : 매개변수 리스트 요소를 합쳐서 하나의 문자열로 반환

from itertools import permutations
def solution(numbers):
    a = set()
    # 에라토스테네스체 채우기
    for k in range(len(numbers)):
        a |= map(int, map("".join, permutations(numbers, k+1)))
    a -= set(range(0,2))

    # 에라토스테네스체 빼기
    for i in range(2, int(max(a)**0.5)+1):
        a -= set(range(i*2, max(a)+1, i))
    
    return len(a)

에라토스테네스의 체 참고 블로그