(8) DP

April 11, 2023

DP란? 문제에 대한 정답이 될 가능성이 있는 모든 해결책을 (완전탐색인데), "체계적"이고 "효율적"으로 탐색하는 풀이법을 말합니다.

DP란?

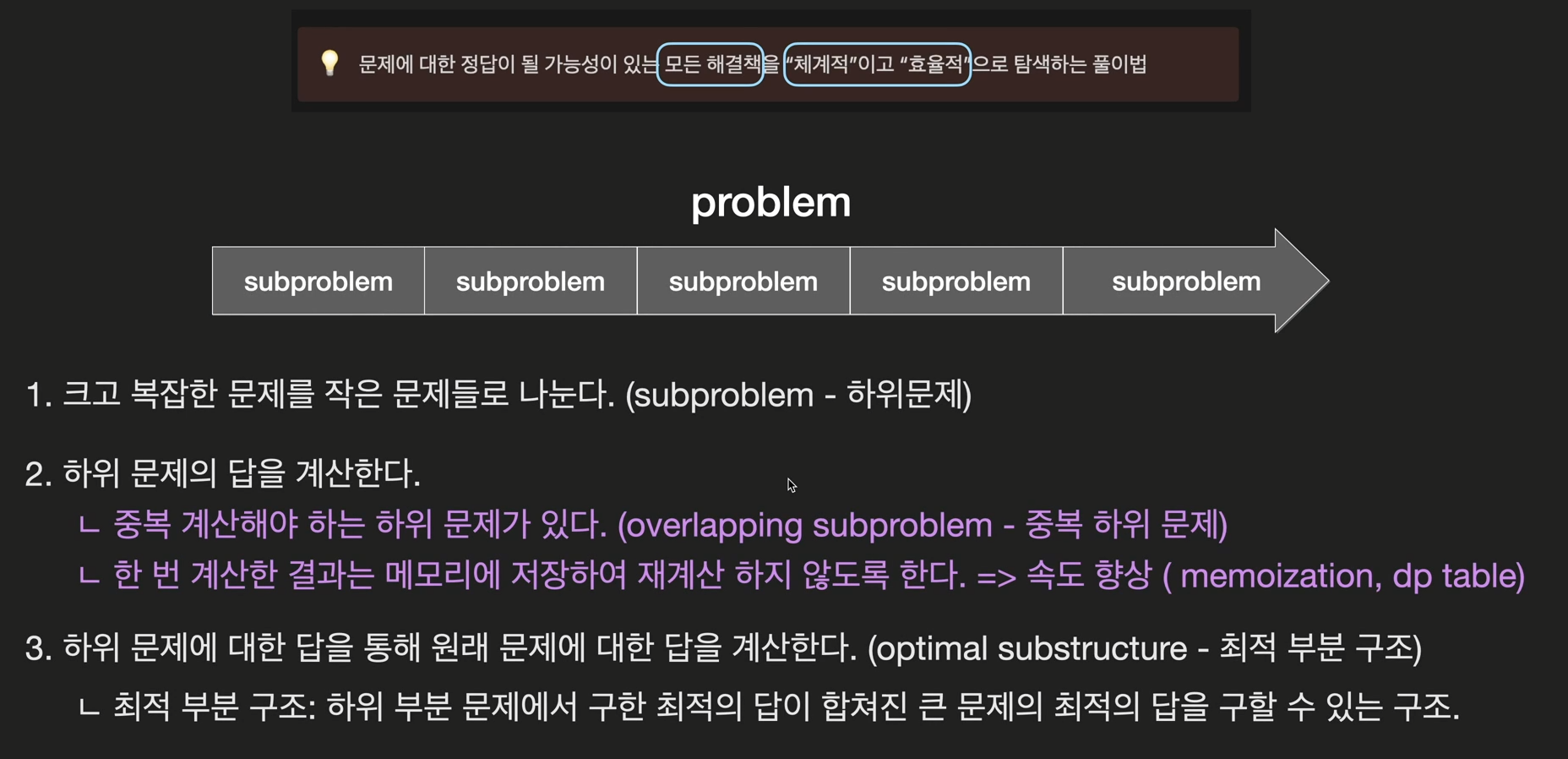
- Overlapping subproblem

- Optimal substructure

위에 두 가지 조건이 성립하면 DP 문제입니다.

DP는 어려운 개념은 아니지만, DP인지 알아차리는 게 어렵기 때문에, 많은 유형을 접하면서 체화하는게 좋습니다.

1. 구현 방법 : Top down vs Bottom up

DP를 재귀로 구현하면 Top-down이고, 반복문으로 구현하면 Bottom-up입니다.

DP는 재계산을 하지 않는 것이며, 메모리에 저장해야 합니다.

Top-down 방식은 메모이제이션(memoization),
Bottom-up 방식은 tabulation(DP table)이라고 많이함.

memoization과 tabulation은 차이가 없고, DP 방식에 따른 명칭 차이입니다. 구현은 dictionary나 list로 합니다.

(1) 비교

탑다운vs바텀업

이렇게 짜면, 좀 쉽습니다.
(1) 완전탐색(재귀)로 짜고 -> (2) Memoization으로 Top-down 구현 (3) Stackoverflow 등 문제가 생기면 Bottom-up으로 바꿔서 구현

(2) 예제 : 피보나치 수열

피보나치 수열 문제를 예시로 보겠습니다.

재귀(DFS)로 풀면? O(2^n)

def fibo(n):
  if n == 1 or n == 2:
      return 1
  return fibo(n-1) + fibo(n-2)

DP로 풀면, 시간복잡도를 O(n)으로 줄일 수 있습니다. (execution tree를 보면 2n) 중복된 문제를 메모리에 저장하여 재계산을 막기 때문입니다.

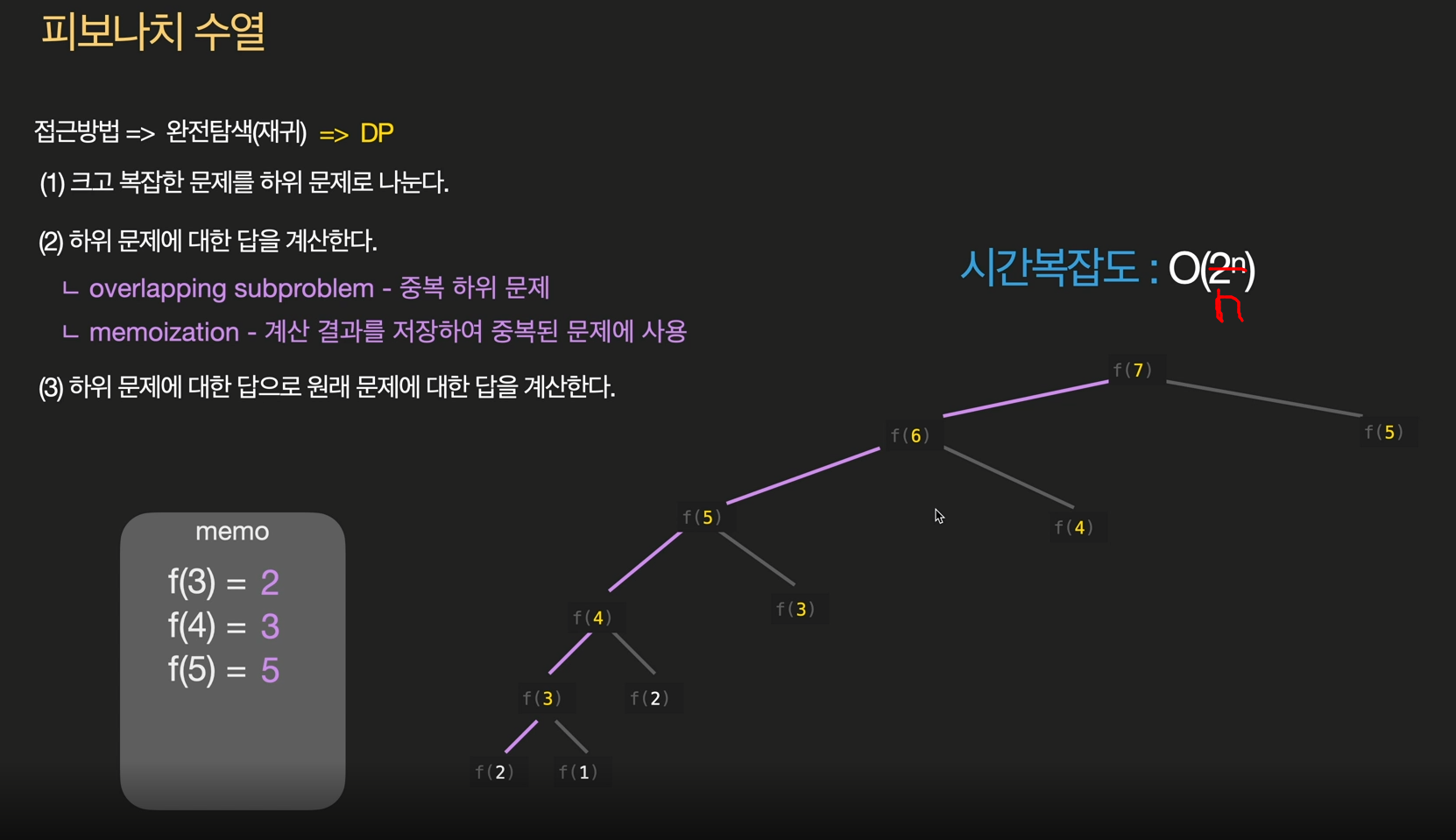
Top-down DP로 풀면? O(n)
```
memo = {1: 1, 2: 1} 
def fibo(n):
  if n not in memo:
      memo[n] = fibo(n-1) + fibo(n-2)
  return memo[n]
```
재귀를 활용해서 위에서부터 아래로 나눠서 구하는 형태이지만,
실제로는 아래에서부터 채워져 더하는 방식입니다.

Bottom-up DP로 풀면? O(n)

def fibo(n): 
  dp = {1: 1, 2: 1}
  for i in range(3, n+1):         # for loop
      dp[i] = dp[i-1] + dp[i-2]
  return dp[n]

메모리에 처음(base case)부터 시작(저장)해서, 메모리에 저장된 값을 꺼내서 더하는 방식입니다.

2. DP Summary

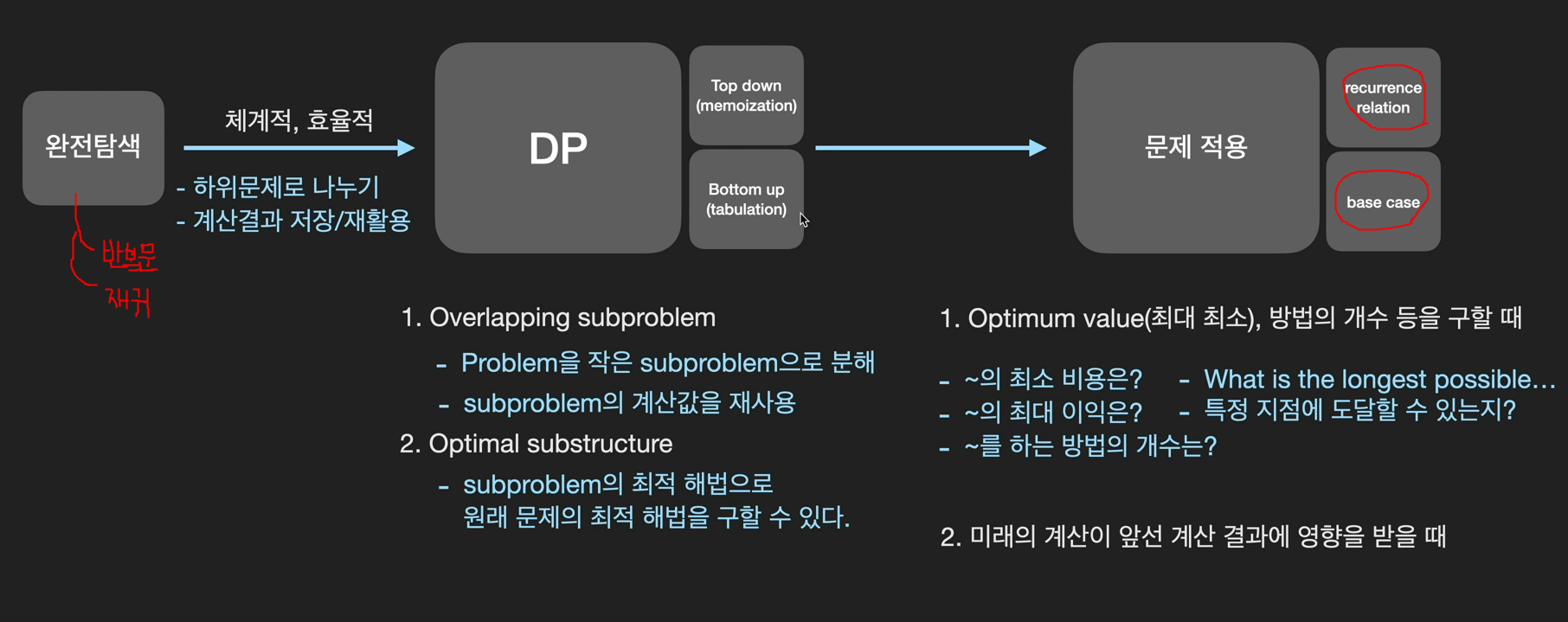
문제 풀면서, 개념도의 이해를 체화하는 반복 과정이 필요합니다. DP_Summary

분할정복은, 미래의 계산이 앞선 계산 결과에 영향을 주지 않는 다는 점에서 DP와 다릅니다.

3. DP 예제

DP는 이론 이해보다는 DP임을 알아차리가 어려울 수 있습니다. 예제를 확인해보겠습니다.

🍓 Climbing Stairs 문제

제한사항 : 1 <= n <= 45
재귀로 풀면?

class Solution:s
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        if n == 2:
            return 2

        return climbStairs(n-1) + climbStairs(n-2)     

Top-down DP로 풀면?

class Solution:
    def climbStairs(self, n: int) -> int:
        memo = {1 : 1, 2 : 2}
        def cs(n):
            if n not in memo:
                memo[n]= cs(n-1) + cs(n-2)
            return memo[n]
        
        return cs(n)

Bottom-up DP로 풀면?

class Solution:
    def climbStairs(self, n: int) -> int:
        dp = {1 : 1, 2 : 2}
        for i in range(3,n+1):
            dp[i] = dp[i-1] + dp[i-2]
        return dp[n]

🍓 Coin Change 문제 ⭐

제한사항 : 0 <= amount <= 10^4, 1 <= coins.length <= 12
예외처리 : 1 <= coins[i] <= 2^31 - 1
접근방법 : dp[i]는 i원을 모으기 위해 필요한 동전 개수
Bottom-up DP : 배수의 관계가 아닐 수 있으므로 greedy문제가 아닌 DP문제입니다.
시간복잡도 : O(n) = O(10^4)

class Solution:
    def coinChange(self, coins, amount: int) -> int:
        dp = [2**31]*(amount+1)
        dp[0] = 0
        for coin in coins:
            for i in range(coin, amount+1):
                dp[i] = min(dp[i], dp[i-coin]+1)
        
        if dp[amount] == 2**31:
            return -1

        return dp[amount]

sol = Solution()
print(sol.coinChange([1,3,5], 7))

[(번외) 동전 배수 문제 접기/펼치기]

🍓 (번외) 11047번: 동전 0

동전이 배수 관계라고 한다면, 나누어 떨어지지 않는 경우가 없기 때문에 간단합니다.

## 백준 Style
# n, amount = map(int, input().split())
# coins = []
# for i in range(n):
#     coins.append(int(input()))
result = 0
coins = coins[::-1]     # 내림차순 정렬
for i in range(n):
        if amount // coins[i] > 0:
            result += amount // coins[i]
            amount = amount % coins[i]
return result

🍓 Unique Paths 문제

제한 사항 : 테스트케이스 답이 2*10^9 = n
접근 방법 : 완전 탐색으로 풀면 시간복잡도 초과이네? 그러면, 메모리를 사용해서 DP로 풀까?

헷갈리네요, Top-down과 Bottom-up은 완전탐색 아닙니다! 완전탐색(BFS,DFS)의 시간복잡도 문제를 해결하기 위해 Memoization하는 방법 입니다.

DFS 완전탐색 으로 풀면?

사실, 수학적으로 접근하면 수식으로 바로 풀 수 있습니다. (m+n-2)C(m-1) = (198)C(99) , 그래서 문제에서 2*10^9 이렇게 제한사항으로 주었네요!

Graph에서 DFS랑 비슷한데, 다만 단방향(하,우)의 경우의 수 구하기 문제이므로 visited 쓰면 안됩니다.

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        def dfs(x, y):
            if x == n and y == m:
                return 1
            count = 0
            if x+1 < n:
                count += dfs(x+1,y)
            if y+1 < m:
                count += dfs(x,y+1)
            return count

DP로 풀면, O(M*N)입니다. 굉장히 강력한 알고리즘이네요!
풀이는 다음과 같습니다.

Top-down 으로 풀면?

가장자리는 1로 초기화하고 수행하였습니다.

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        memo = {}
        for y in range(m):
            memo[(0,y)] = 1
        for x in range(n):
            memo[(x,0)] = 1
        
        def pathCount(coordinate):
            if coordinate not in memo:
                x, y = coordinate
                memo[(x,y)] = pathCount((x,y-1)) + pathCount((x-1,y))
            return memo[coordinate]
        
        return pathCount((n-1,m-1))

Bottom-up 으로 풀면?

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        dp = {}
        for y in range(m):
            dp[(0,y)] = 1
        for x in range(n):
            dp[(x,0)] = 1
            
        for x in range(1,n):
            for y in range(1,m):
                dp[(x,y)] = dp[(x-1,y)] + dp[(x,y-1)] 
                
        return dp[(n-1,m-1)]

🍓 Min Cost Climbing Stairs 문제

제한 사항 : 2 <= cost.length <= 1000
시간 복잡도 : O(n)

DFS 완전탐색 으로 풀면?

def dfs(n):
  if n == 0 and n ==1:
      return 0
  return min(dfs(n-1)+cost[n-1], dfs(n-2)+cost[n-2])

하지만, DFS로 풀면 O(2^n)이므로 시간초과가 걸립니다.

Top-down 으로 풀면?

Bottom-up 으로 풀면?

class Solution:
  def minCostClimbingStairs(self, cost: List[int]) -> int:
      n = len(cost) 
      cost.append(0)
      dp = {0: cost[0], 1: cost[1]}
      for i in range(2,n+1):
          dp[i] = min(dp[i-1], dp[i-2])+cost[i]
      return dp[n]

다음에는 힙/우선순위 큐 에 대해서 포스팅 하겠습니다 :)

해당 시리즈의 포스트는 인프런에서 제공하는 개발남노씨의 코딩테스트 강의 를 바탕으로 작성하였습니다.