(10) BinarySearch

이분탐색의 시간복잡도는 O(logN)입니다.

middle을 업데이트하면서 target값 찾기

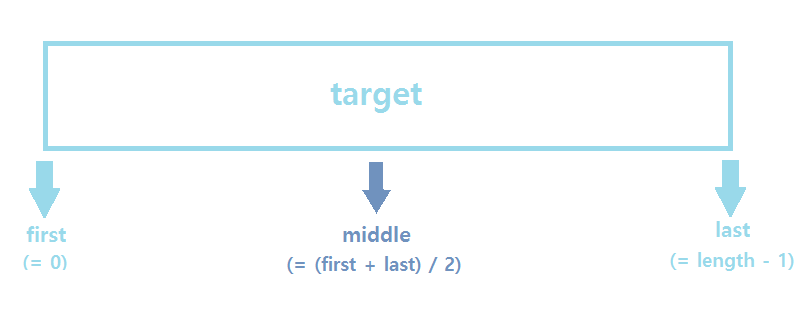
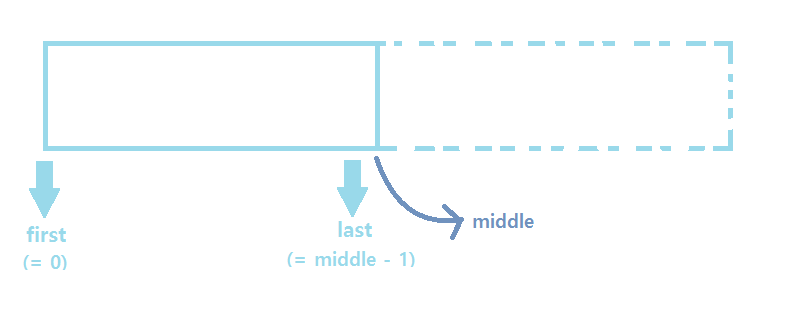
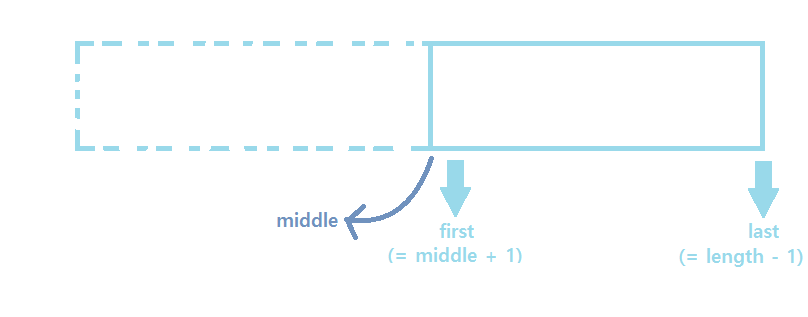
mid값이 아니므로, left와 rigth는 mid의 +-1로 업데이트합니다.

코테 문제

🍓 1. Binary Search

• 문제 상황 : 오름차순으로 정렬된 배열에서 target값을 찾아야 합니다.

• 제한 사항 : 알고리즘은 반드시 O(logn) 이어야 합니다.

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums)-1
        
        # 예외처리
        if len(nums) ==1:
            if nums[0] == target:
                return 0
            else:
                return -1        
        
        while (left <= right):
            mid = (left + right)//2
            if target == nums[mid]:
                return mid
            elif target < nums[mid]:
                right = mid - 1
            else:
                left = mid + 1
        return -1

🍓 2. 입국심사

이진탐색을 문제에 적용하려면 우선, (1) left - right 범위 설정 (2) 중간값 검증 어떻게 할지 생각해야합니다!

• 이분 탐색의 범위 설정

  최소시간과 최대시간 설정

  최대시간은 (가장 느린 심사관의 심사 시간) * (사람의 수)

• 중간값 검증

  각 심사관의 (중간값//심사시간) 의 총합이 == 사람수

def solution(n, times):
    left, right = 1, max(times) * n

    def count(time):
        nums = 0
        for a in times:
            nums += time // a
        return nums

    answer = 0
    while left <= right:
        mid = (left + right) // 2
        counted = count(mid)
        if n == counted:
            answer = mid  # Save the result if the count matches
            right = mid - 1  # Still try to find a smaller value
        elif n < counted:
            right = mid - 1
        else:
            left = mid + 1

    # If no exact match is found, return the saved result or the left value
    return answer if answer else left

🍓 3. 징검다리 건너기 (Lv.3)

• 문제 상황 : 니니지 친구들이 무제한으로 있을 때, 징검다리를 건널 수 있는 친구들의 최대 인원 수를 구하는 문제입니다. 징검다리 돌은 밟을 수 있는 숫자가 각각 정해져 있으며, 0이 되면 밝을 수 없고 다음 돌로 jump할 수 있습니다. jump 가능한 수는 k로 주어집니다.

• 제한 사항 : 1<= stones의 배열의 길이, k <= 2*10^5

• 문제 이해 : 0인 징검다리 돌이 k개 연속될 경우, 징검다리 건너기 종료! stones 배열의 길이가 매우 크므로 원소를 하나씩 차감해주면, 타임오버가 걸립니다.

• 문제 접근 : 이진 탐색 O(logN)

(1) 나의 풀이 : 정확성 100, 효율성 0

처음에는, 원소를 하나씩 차감하면서, 연속으로 0인 돌이 k가 생기는지 확인하는 방식으로 코드를 짰습니다.

[나의 풀이 접기/펼치기]

def solution(stones, k):
    answer = 0
    cur = 0
    n = len(stones)
    
    while True:
        if cur == n:
            answer += 1
            cur = 0
        
        if stones[cur] != 0:
            stones[cur] -= 1
        
        else:
            nothing = True
            for i in range(1,k):
                if cur + i == n:
                    answer += 1
                    cur = -1
                    nothing = False
                    break

                if stones[cur+i] != 0:
                    cur += i
                    stones[cur] -= 1
                    nothing = False
                    break
            if nothing:
                break
        
        cur += 1
          
    return answer

(2) 이진탐색으로 풀기

O(nlongm), n: 디딤돌개수, m: 디딤돌의 최대값

# 최소/최대 idx를 가지고, 친구들의 수(M)를 찾기

def solution(stones, k):
    # 예외처리
    if k == 1:
        return min(stones)
    
    # M의 최소와 최대를 setting
    left = 1
    right = max(stones)
        
    # M이 답이라고 할 때, M-1에서 (k-1)개의 연속된 0이 있다. 
    def binaryCheck(mid):
        zeroCount = 0
        for v in stones:
            if v < mid:
                zeroCount += 1
            else:
                zeroCount = 0   # 연속되는 0만 의미가 있으므로
            if zeroCount >= k:  # k-1개까지 가능
                return False
        return True 
    
    while left < right-1 :
        mid = (left+right)//2
        if binaryCheck(mid):
            left = mid
        
        else:
            right = mid
            
    return left