PCA 와 K-means Clustering 의 관계

결론

So k-means can be seen as a super-sparse PCA.

보통, k-means clustering 전에 노이즈 감소를 위해 PCA (principal component analysis)를 적용한다.

(1) Projection / PCA

-개념

\[\vec{e}^*=arg max_{\vec{e}}Var(M\vec{e})\]

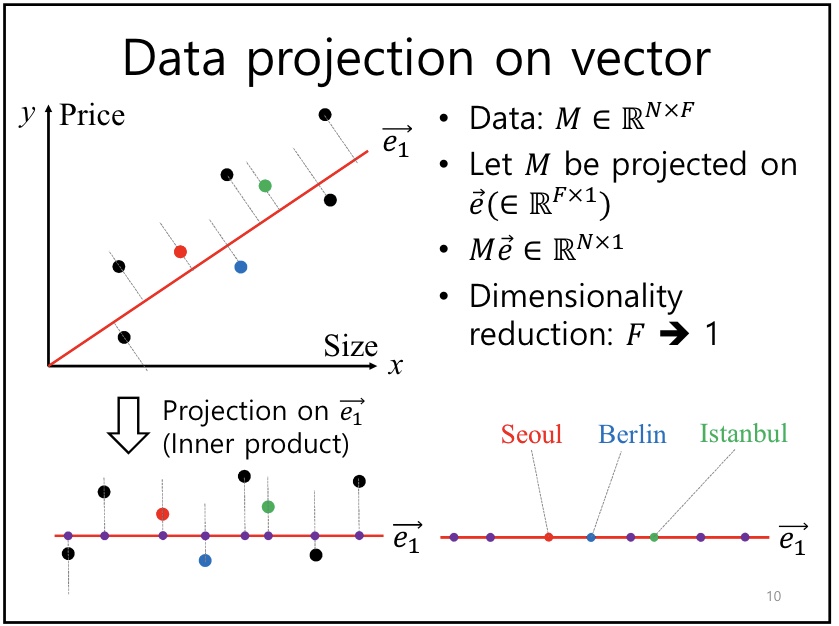
Projection 시, 데이터set인 M을 가장 잘 설명하는 (데이터가 골고루 분산되도록 하는) vector(axis) e 를 찾고자 한다.

왜냐하면 데이터의 차원 축소 시 정보 손실을 최소화하기 위해서이다.

다시 말해, Var(Me) 분산식 을 최대로 하는 eigen vector e 를 찾고자 한다.

분산식은 공분산 행렬 $\sum$ 로 나타낼 수 있으며, 분산식은 곧 eigen value $\lambda$ 를 의미한다.

\[Var(M\vec{e})=\vec{e}^T \Sigma \vec{e}=\lambda\]

이는 다음과 같은 풀이과정으로 도출된다.

\[Var(M\vec{e})={\operatorname{1}\over\operatorname{N}}\sum_{i=1}^N(M\vec{e}-E(M\vec{e}))^2\] \[Var(M\vec{e})={\operatorname{1}\over\operatorname{N}}\sum_{i=1}^N(M\vec{e})^2 \quad s.t. E(M\vec{e})=0\] \[Var(M\vec{e})={\operatorname{1}\over\operatorname{N}}\sum_{i=1}^N(M\vec{e})(M\vec{e})={\operatorname{1}\over\operatorname{N}}\sum_{i=1}^N(M\vec{e})(M\vec{e}) \quad (Bassel's correction)\] \[Var(M\vec{e})={\operatorname{1}\over\operatorname{N}}\vec{e}^TM^TM\vec{e} =\vec{e}^T{\operatorname{M^TM}\over\operatorname{N}}\vec{e}=\vec{e}^T\sum\vec{e}=\vec{e}^T\lambda\vec{e}=\lambda\]

Principal projection vector (axis) 는 eigenvector e 이다. 이때의 분산이 eigen-value $ \lambda\ $이며, 이는 데이터가 얼마나 spread 되어있는지를 의미한다.

-코드

코드로 보면 다음과 같다.

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x= np.random.normal(scale=8, size=200)
y= x+np.random.normal(scale=3, size=200)

x= x-np.mean(x)
y= y-np.mean(y)
data= np.array([x,y])

plt.figure()
plt.scatter(x,y)
plt.show()

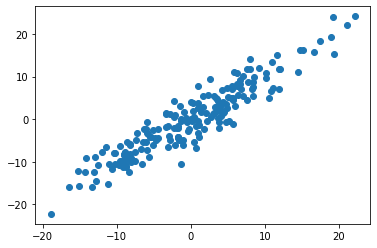
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(data.T)
print(pca.components_.T)

#[[ 0.69246889  0.72144774]
#[ 0.72144774 -0.69246889]]

pca.components는 feature space 상에서, principal vectors를 의미한다.

이는 데이터의 분산이 최대가 되도록 하는 방향을 의미한다. (이 경우는, $ \lambda$ 11.11)

해당 component는 explain_variance에 의한 순서이다.

np.sqrt(pca.explained_variance_)

#array([11.11412819,  2.05445079])

any_num = 3     # (arbitrary) the length of line
sigma3_evalue= any_num*np.sqrt(pca.explained_variance_[0])
sigma3_evalue_arr= np.array([[-sigma3_evalue, sigma3_evalue]]) # (arbitrary) for make diagonal line
eigenvector = np.array([pca.components_[0]]).T
evector_x, evector_y = np.dot(eigenvector, sigma3_evalue_arr)

plt.figure()
plt.scatter(x,y)
plt.plot(evector_x, evector_y)
plt.show()

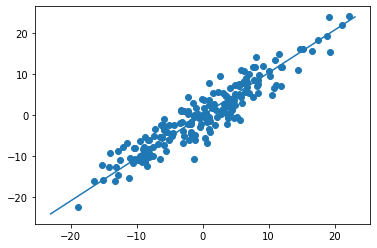
(2) K-means clustering

-군집 vs 분류

분류는 supervised learning(지도학습)으로 label(y)값이 있지만,
군집은 unsuperviesd learning(비지도 학습)으로 label이 사전에 알려져 있지 않을 때 사용하는 알고리즘이다.

-코드

# k-means clustering
k=5
kmeans = KMeans(n_clusters=k, random_state=42)
X_kmeans = kmeans.fit_transform(X_pca)
y_pred = kmeans.fit_predict(X_pca)
X_kmeans, y_pred

# visualize by TSNE
tsne = TSNE(n_components=3, random_state=42)
X_tsne = tsne.fit_transform(X_kmeans)

# 3-D graph
fig = plt.figure()
ax = fig.gca(projection='3d')
fig.set_size_inches(18.5,10.5)
ax.scatter(X_tsne[:,0], X_tsne[:,1], X_tsne[:,2], c=y_pred, cmap="jet")

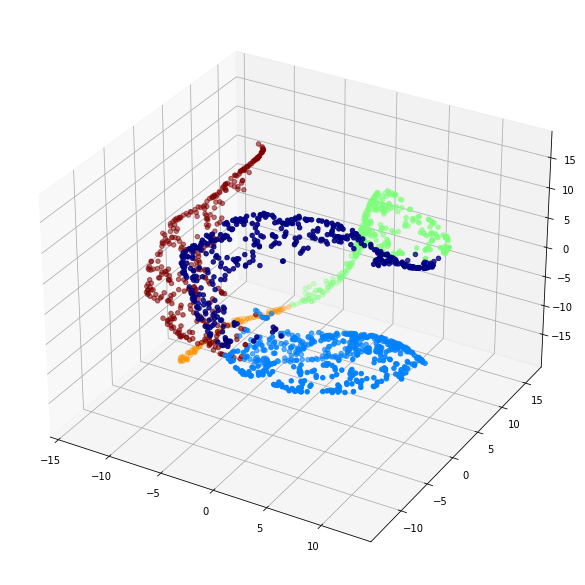
(3) Relation between PCA and K-means

k-means clustering 과 PCA 는 각각 적은 수의 centroid vector, eigenvector 의 선형 조합을 찾는다는 점에서 다르지만,
학습에 사용되는 Objective function 이 같기 때문에 (단, k-means에는 제약조건이 추가), 꽤 같은 결과를 갖는다.

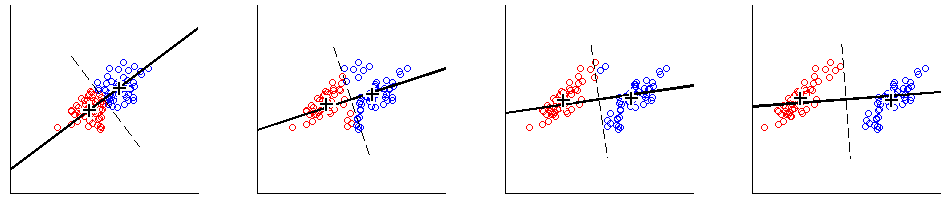
자세한 설명과 증명은 다음 블로그에서 참고.
https://stats.stackexchange.com/questions/183236/what-is-the-relation-between-k-means-clustering-and-pca