[CV_basic] 게시글은 CMU의 computer vision 강의를 토대로 작성하였습니다.
http://www.cs.cmu.edu/afs/cs/academic/class/15385-s12/www/
결론
이미지 프로세싱은 low-level 컴퓨터비전(CV)에 해당한다.
이미지는 함수로 표현할 수 있으며, 컬러 이미지는 vector-valued 함수이다.
NN은 필터(=커널)의 적합한 값을 학습하며, 필터도 함수로 볼 수 있다.
이미지 프로세싱은 함수(기존 이미지)와 함수(필터)를 통해 새로운 함수(새로운 이미지)를 만드는 것이다.
1. 이미지 프로세싱 / 컴퓨터비전
컴퓨터 비전의 계층은 다음과 같다.
| level | process | e.g. |
|---|---|---|
| Low | image -> image | image_processing, edge-detection, colorization, |
| Mid | image -> features | boundary-detection, segmentation |
| High | image -> semantics | object-recognition, image-captioning |
-이미지의 동물이 개인지 고양이인지 구분하거나, 이미지의 상황에 대해 자막을 달아주는 것은 고레벨의 CV 으로, 이는 이미지의 의미(semantics)를 파악해야 한다.
-이미지의 경계선을 파악해 경계선만 따거나, segmentaion 하는 것은 이미지의 feature를 파악해야하는 중간레벨의 CV로 분류할 수 있다.
-단순히 image를 반전시키거나, 흐릿한 사진을 선명하게 하거나, 혹은 흑백을 컬러 사진으로 바꾸는 것은 이미지의 픽셀값을 연산하여 처리할 수 있는 저레벨의 CV에 해당한다.
이미지 프로세싱은 저레벨의 컴퓨터비전에 해당한다.
2. 이미지 프로세싱
하나의 이미지는 하나의 함수로 생각할 수 있다.
$ f : R^2 \to R $
$ f(x,y) = [0, 255] $
컬러 이미지의 경우는 vector-valued 함수로 생각할 수 있다.
이미지 프로세싱을 기존의 함수 $f$ 에 변환 $T$ 을 주어 새로운 함수 $g$ 를 얻는 것으로, 다음과 같이 식으로 표현할 수 있다.
$ g = T(f) $
변환 $T$ 는 두 가지로 분류할 수 있다. (1) Point operation, (2) Neighborhood operation 이다.
(1) Point operation
각 픽셀값에 동일한 값으로 가감승제하여 새로운 이미지를 얻는다.

https://www.programmersought.com/article/70807541818/
(2) Neighborhood operation
주변 픽셀값에 대한 고려가 필요할 때 인접작업(neighborhood operation)으로 이미지를 처리한다.
필터(=커널)을 정의하고, original 이미지를 convolution 하는 것을 말한다.
합성곱(convolution operation) 을 동일하게 쓰고, kernel만 바꾸면 새로운 이미지를 얻는다.
NN이 필터의 각 값을 스스로 배운다.
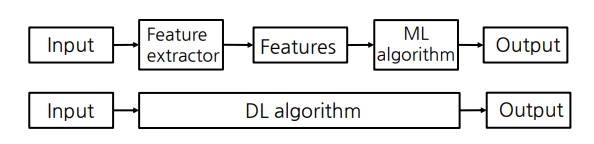
3. CV에서 머신러닝과 딥러닝
실제로 쓰이기는 딥러닝이 많이 쓰인다.
그 이유는 딥러닝은 이미지에서 좋은 features를 알아서 찾아주기 때문이다. 하지만 작동원리를 파악하기가 어렵다. 따라서 컴퓨터비전의 원리를 알기 위해서는 머신러닝 알고리즘 사용한다.
https://cse.snu.ac.kr/professor/%EA%B9%80%EA%B1%B4%ED%9D%AC
Accuracy-Interpretability Tradeoff!!
4. 합성곱(convolution)과 교차상관(cross-correlation)
(1) Convolution
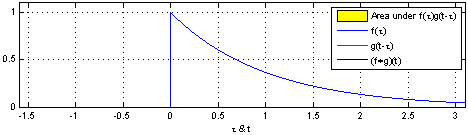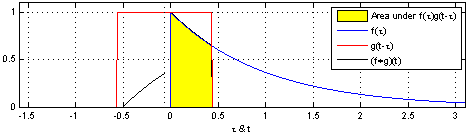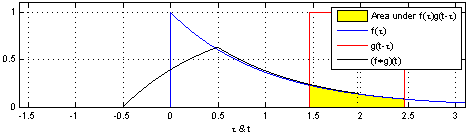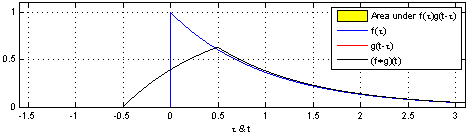
convolution 연산이란, 두 개의 함수를 통해 새로운 함수를 산출하는 연산으로 두 함수 중 하나의 함수를 reverse 하고 -t 만큼 shift 한 후 두 함수의 값을 곱하여 더한 값이다.
$h(t) = (f*g)(t) = \int_{-\infty}^\infty f(\tau)g(t-\tau)d\tau$
즉, Convolution은 단순 교집합 면적이 아닌, 각 값을 곱한 면적이다.
https://cse.snu.ac.kr/professor/%EA%B9%80%EA%B1%B4%ED%9D%AC
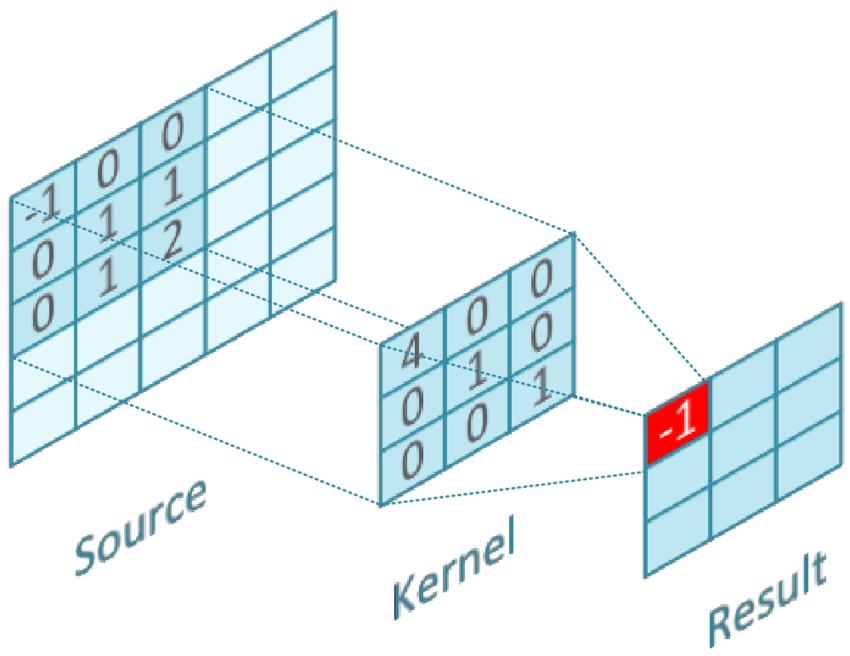
2D convolution 연산은 다음과 같다.
$h(i,j) = \displaystyle\sum_m\sum_n f(m,n)g(i-m, j-n)$
DOI: 10.13140/RG.2.2.11700.35207
(1) horizontal, (2) vertical 로 각각 flip(reverse) 하고, (3)두 함수의 값 곱하고 (4) 더한다.
(2) cross-correlation
convolution 과 거의 유사하다. 다만, flip 하지 않고, 바로 (3)두 함수의 값 곱하고 (4) 더한다.
따라서 1-D, 2-D 식은 다음과 같다.
$h(t) = (f*g)(t) = \int_{-\infty}^\infty f(\tau)g(t\color{red}+\color{balck}\tau)d\tau$
$R(i,j) = \displaystyle\sum_m\sum_n f(m,n)g(\color{red}{m-i, n-j}\color{balck})$
cross-correlation은 주로, template matching 에 사용한다.

https://cse.snu.ac.kr/professor/%EA%B9%80%EA%B1%B4%ED%9D%AC
이러한 naive-cross-correlation 은 문제점을 갖는다. 이는 다음 그림을 통해 알 수 있다.

https://cse.snu.ac.kr/professor/%EA%B9%80%EA%B1%B4%ED%9D%AC
템플릿과 원래 이미지의 signal이 유사한 값을 찾아야 하므로, A에서 cross-correlation이 최대여야 하는데 위의 경우에는 C값 자체가 크므로 C에서 최대가 된다.
이러한 문제를 고려한 cross-correlation을 Normalized correlation 이라 하며, 식은 다음과 같다.
$R(i,j) = \frac{\displaystyle\sum_m\sum_n f(m,n)t(m-i, n-j)}{\displaystyle{[\sum\sum f(m,n)^2]}^{1/2}{[\sum\sum t(m-i, n-j)^2]}^{1/2}}$
5. 가우시안 스무딩 (Gaussian Smoothing)
가우시안 스무딩이란, 컨볼루션 커널이 gaussian kernel 인 이미지 프로세싱이다.
이미지의 edge를 스무딩 하거나 블러처리 할 때 사용한다.
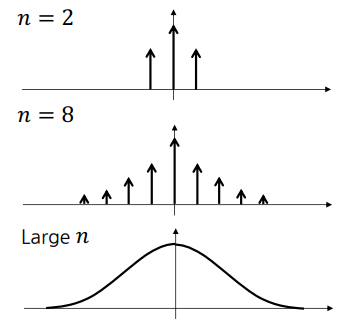
가우시안 스무딩은, 특정 point를 기준으로 주변 픽셀 값을 repeated averaging 한 것이다.
특정 point에 가까울수록 weight이 높고, 멀수록 낮다.
https://cse.snu.ac.kr/professor/%EA%B9%80%EA%B1%B4%ED%9D%AC
*median 필터
median 필터는 특정 점의 주변 픽셀의 값을 sort 해서, 그것의 중간 값으로 값을 바꾼다.
이는 non-linear 하므로 컨볼루션 연산으로 구현되지 않고, horizontal 혹은 vertical artifact (선 같은 것) 가 생기는 단점이 있다.
가우시안 필터는 다음과 같다.
$h(i,j) = \displaystyle\frac{1}{2\pi\sigma^2}exp(-\frac{i^2+j^2}{2\sigma^2 })$
가우시안 필터의 컨볼루션 즉, 가우시안 스무딩은 다음과 같다.
$g(i,j) = \displaystyle\frac{1}{2\pi\sigma^2}\sum_{m=1}\sum_{n=1}exp(-\frac{i^2+j^2}{2\sigma^2})f(i-m,j-n)$
이는 m,n에 대한 필터의 곱으로 separable 하다!
$g(i,j) = \displaystyle\frac{1}{2\pi\sigma^2}\sum_{m=1}exp(-\frac{i^2}{2\sigma^2})\sum_{n=1}exp(-\frac{j^2}{2\sigma^2})f(i-m,j-n)$
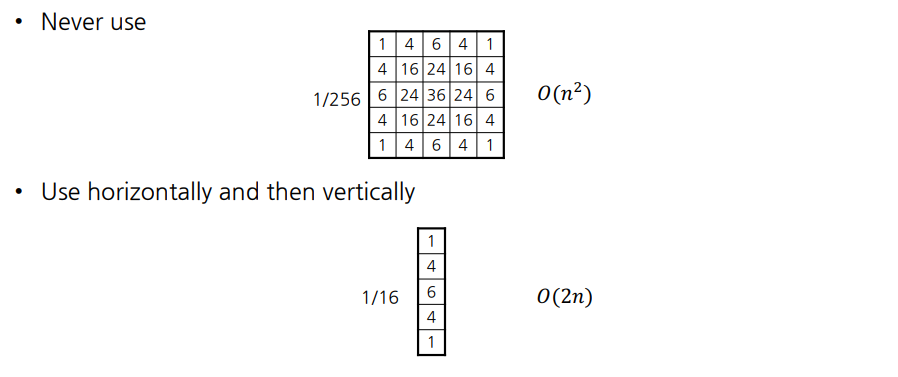
즉, 2d filter는 1d filter를 horizontal, vertical로 두 번 하는 것 과 같다.
https://cse.snu.ac.kr/professor/%EA%B9%80%EA%B1%B4%ED%9D%AC
시간복잡도가 1d filter일 때 O(2n)으로 더 낮기 때문에, 가우시안 스무딩은 1차원 가우시안 필터로 두 번 해야한다.
이상입니다. 설명이 부족한 부분이나 오류가 있으면 댓글 남겨주세요.

Leave a comment