(5) Mosaics (Warping)
각 veiw point의 이미지를 합쳐서 한 장의 파노라마 사진을 만들려면 어떻게 어떻게 해야할까요? Mosaic을 하면 됩니다.
두 이미지간의 매칭되는 특징점(keypoint)으로 homography matrix을 구한 후, 이를 통해 warping 한 후 이미지를 이어붙이면 됩니다.
1. Keypoint 와 homography matrix
이미지의 특징이 되는 점을 특징점(keypoint)이라고 합니다. 특징점은 보통 물체의 모서리나 코너입니다.
따라서 대부분의 특징점 검출 알고리즘은 코너 검출을 바탕으로 합니다. 대표적으로 해리스 코너 검출(Harris Corner Detection), 이에 affine 변화까지 고려한 시-토마시 검출(Shi & Tomasi Detection), 그리고 DoG를 통해 스케일까지 고려한 SIFT-DoG 등이 있습니다.
(1) 특징점 ${x_i ,x^{‘}_i}$을 직접 지정

# 왼쪽 이미지
p_in = np.array([[375,98],[358,109],[265,137],[207,139],[146,180],[121,224],[371,250]])
# 오른쪽 이미지
p_ref = np.array([[207,267],[217,232],[281,137],[330,103],[331,50],[307,22],[107,93]])
특징점의 scale을 맞추기 위해서 두 이미지간의 특징점을 정규화하였습니다.
sum1 = 0.
sum2 = 0.
# sum of square of distance from each point to the average point
for i in range(0, n):
sum1 += (p1[i,0] - avg_x1) ** 2 + (p1[i,1] - avg_y1) ** 2
sum2 += (p2[i,0] - avg_x2) ** 2 + (p2[i,1] - avg_y2) ** 2
s1 = math.sqrt(2) * n / math.sqrt(sum1)
s2 = math.sqrt(2) * n / math.sqrt(sum2)
T1 = s1 * np.array([[1, 0, -avg_x1],[0, 1, -avg_y1],[0, 0, 1/s1]])
T2 = s2 * np.array([[1, 0, -avg_x2],[0, 1, -avg_y2],[0, 0, 1/s2]])
p1 = np.pad(p1, ((0,0),(0,1)), 'constant', constant_values = 1)
p2 = np.pad(p2, ((0,0),(0,1)), 'constant', constant_values = 1)
p1 = np.dot(p1, np.transpose(T1[0:2,:]))
p2 = np.dot(p2, np.transpose(T2[0:2,:]))
(2) 이미지를 warping하기 위해서 3차원 변환행렬인 Homography 행렬 계산
지정한 ${x_i ,x^{‘}_i}$ 에 대한 Homography 행렬은 다음과 같은 식으로 표현합니다.
\[\begin{bmatrix}x^{'}\\ y^{'}\\ 1\\ \end{bmatrix} = \alpha H\begin{bmatrix}x\\ y\\ 1\\ \end{bmatrix}\] \[H = \begin{bmatrix}h_1 & h_2 & h_3\\ h_4 & h_5 & h_6 \\ h_7 & h_8 & h_9 \\ \end{bmatrix}\]따라서, 두 대응점의 z가 같다고 가정했기 때문에 H행렬을 구할 때 고려하지 않아도 됩니다. 즉, $h_9$는 스케일과 관련된 값으로 1 또는 사용할 스케일 값을 적용할 것이기 때문입니다.
문제를 풀기 위해서, Homogeneous Linear equation 형태로 변형하여 선형연립방정식으로 나타내고 최소자승법 으로 matrix로 구할 수 있습니다.
A. Homogeneous Linear Equation
\[A_ih=0\] \[A_i =\begin{bmatrix}-x&-y&-1&0&0&0&xx^{'}&yx^{'}&x^{'}\\ -x&-y&-1&0&0&0&xx^{'}&yx^{'}&x^{'}\\ \end{bmatrix}\]H행렬의 미지수가 8개이므로 ($h_9$=1), 8개의 식이 필요하므로 H를 구하기 위해서는 최소 4개가 필요합니다.
\[\begin{bmatrix}-x_1&-y_1&-1&0&0&0&x_1x^{'}_1&y_1x^{'}_1&x^{'}_1\\ 0&0&0&-x_1&-y_1&-1&x_1y^{'}_1&y_1y^{'}_1&y^{'}_1\\ -x_2&-y_2&-1&0&0&0&x_2x^{'}_2&y_2x^{'}_2&x^{'}_2\\ 0&0&0&-x_2&-y_2&-1&x_2y^{'}_2&y_2y^{'}_2&y^{'}_2\\ -x_3&-y_3&-1&0&0&0&x_3x^{'}_3&y_3x^{'}_3&x^{'}_3\\ 0&0&0&-x_3&-y_3&-1&x_3y^{'}_3&y_3y^{'}_3&y^{'}_3\\ -x_4&-y_4&-1&0&0&0&x_4x^{'}_4&y_4x^{'}_4&x^{'}_4\\ 0&0&0&-x_4&-y_4&-1&x_4y^{'}_4&y_4y^{'}_4&y^{'}_4\\ \end{bmatrix}\begin{bmatrix}h_1\\ h_2 \\ h_3 \\ h_4 \\ h_5 \\ h_6 \\ h_7 \\ h_8 \\ h_9 \\ \end{bmatrix} = \begin{bmatrix} 0\\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}\] \[Ah=0\]따라서, 특징점 n(7)개로 $2n\times9$ matrix를 만들었습니다.
n = p1.shape[0] # keypoint 개수, 7
A = np.zeros((2*n, 9)).astype(float)
for i in range(n):
A[i*2][0] = p2[i][0]
A[i*2][1] = p2[i][1]
A[i*2][2] = 1.
A[i*2][6] = - p2[i][0] * p1[i][0]
A[i*2][7] = - p1[i][0] * p2[i][1]
A[i*2][8] = - p1[i][0]
A[i*2+1][3] = p2[i][0]
A[i*2+1][4] = p2[i][1]
A[i*2+1][5] = 1.
A[i*2+1][6] = - p2[i][0] * p1[i][1]
A[i*2+1][7] = - p2[i][1] * p1[i][1]
A[i*2+1][8] = - p1[i][1]
이렇게 Homogenenous Linear equation 형태로 변형하면, SVD를 이용하여 선형연립방정식을 풀 수 있습니다.
B. SVD를 이용해서 선형연립방정식 풀기
$Ax = 0$ 의 형태는
A의 특이값분해(SVD)를 $A=U\Sigma V^{T}$라 할 때, x(해)는 V의 가장 오른쪽 열벡터 (즉, A의 최소 특이값에 대응하는 right singural vector) 입니다.
[ 특이치에 대한 추가 설명 접기/펼치기 ]
A의 특이치(singular vlaue)는 $A^TA$의 고유값(eigen value)에 루트를 씌운 값이며, $A\vec{v_1}, …, A\vec{v_r}$ 벡터의 길이입니다. $v$는 $A^TA$의 고유 벡터입니다.
U는 ${A\vec{v_1}, …, A\vec{v_r}}$ 을 정규화 한 ${\vec{u_1}, …, \vec{u_r}}$ 벡터가 열들로 이루어진 행렬입니다. A의 left singular vector로 부릅니다.
\[u_i = \frac{1}{\|Av_i\|}Av_i=\frac{1}{\sigma_i}Av_i\] \[U = [u_1, u_2, ..., u_m]\]V는 A의 right singular vector라고 부릅니다.
A행렬의 SVD를 통해 구한 V의 마지막 열이 최소자승(least-square)법에 의한 Homography 입니다.
u, s, v = np.linalg.svd(A) # 행렬분해
H = v[s.shape[0]-1].reshape((3,3)) # Homography
다음과 같은 Homography 행렬을 구할 수 있습니다.
\[\begin{bmatrix}-5.53723803e-01&-7.57213921e-02&2.86499527e+02\\ 1.85636315e-01&-2.44602262e-01&4.63977743e+01\\ -4.78748251e-04&1.53204801e-03&3.74904029e-01\\ \end{bmatrix}\]2. Mosaics
warping 함수 구현
Homography 행렬을 통해 왼쪽 그림을 warping하고, 이를 오른쪽 그림과 이어붙이면 Mosaic이 됩니다.
왼쪽 그림의 모든 픽셀을 mapping하여 이어붙이면 aliasing과 sub-sampling effect 현상이 있으므로, Mosaic 최종 이미지의 크기를 설정하고 이에 해당되는 픽셀을 homography로 변환하여 ref 이미지와 이어붙이는 방법으로 구현했습니다.
# multipling H to 4 corner vertexes of igs_in and divide it to array[2]
p1 = (np.dot(H, [0,0,1])).astype(float)
p1 = (p1 / p1[2]).astype(int)
p2 = (np.dot(H, [igs_in.shape[1]-1, 0, 1])).astype(float)
p2 = (p2 / p2[2]).astype(int)
p3 = (np.dot(H, [0, igs_in.shape[0]-1, 1])).astype(float)
p3 = (p3 / p3[2]).astype(int)
p4 = (np.dot(H, [igs_in.shape[1]-1, igs_in.shape[0]-1, 1])).astype(float)
p4 = (p4 / p4[2]).astype(int)
x_arr = [p1[0], p2[0], p3[0], p4[0]]
y_arr = [p1[1], p2[1], p3[1], p4[1]]
x_n = np.amax(x_arr) - np.amin(x_arr)
y_n = np.amax(y_arr) - np.amin(y_arr)
# warp igs_in to igs_warp
igs_warp = np.zeros((max(igs_ref.shape[0]-1, np.amax(y_arr)-np.amin(y_arr)), max(igs_ref.shape[1]-1, np.amax(x_arr)), 3))
# concatenate igs_ref and igs_merge
igs_merge = np.zeros((max(igs_ref.shape[0]-1, np.amax(y_arr)-np.amin(y_arr)), max(igs_ref.shape[1]-1, np.amax(x_arr)), 3))
H_inv = np.linalg.inv(H)
for y in range(0, y_n):
for x in range(0, x_n):
new = (np.dot(H_inv, np.array([x - np.amin(x_arr), y + np.amin(y_arr), 1.]))).astype(float)
new = (new / new[2]).astype(int)
if 0 <= new[0] < igs_in.shape[1] and 0 <= new[1] < igs_in.shape[0] : # if new point is in igs_in
igs_warp[y,x,:] = igs_in[new[1],new[0],:]
igs_merge[y,x,:] = igs_in[new[1],new[0],:]
igs_merge[-np.amin(y_arr) : -np.amin(y_arr) + igs_ref.shape[0], np.amin(x_arr): np.amin(x_arr) + igs_ref.shape[1], :] = igs_ref
return igs_warp, igs_merge
결과
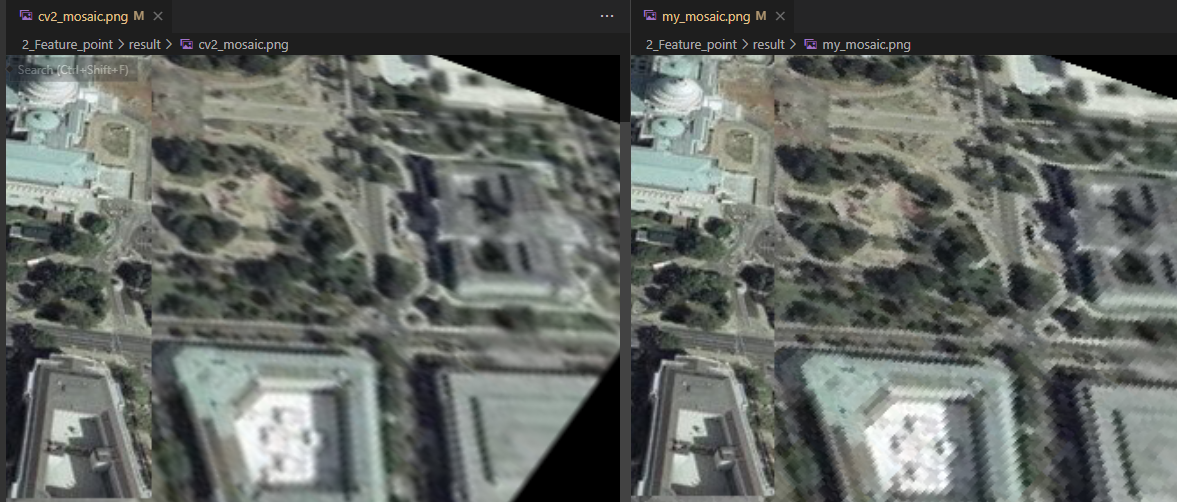
제가 구현한 결과인 warp, merg된 사진을 CV2 라이브러리의 getPerspectiveTransform(), warpPerspective() 함수를 통해 구한 사진과 비교했습니다.


제가 구현한 사진은 cv2의 결과와 비교했을 때 waping된 이미지의 aliasing 정도가 작습니다 (화질이 덜 깨짐).
참고 블로그

Leave a comment