(2) 푸리에 변환

푸리에 변환(Fourier Transformation, FT)는 신호처리, 이미지 및 영상처리에서 다루는 중요한 개념이다.

FT를 통해 얻는 스펙트럼(spectrum) 인, 위상(phase)과 크기(magnitude)를 통해 이미지 및 영상에 대한 spectral analysis가 가능하다.

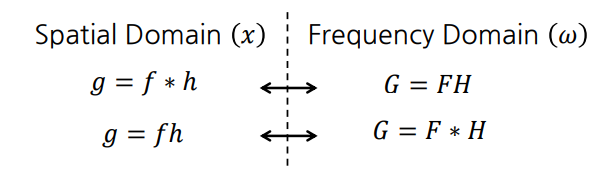
spatial domain (통신 분야에서는 time domain 이라 함) 에서의 Convolution 은 $\Leftrightarrow$ frequency domin 에서의 곱 (multiplication) 과 같다.

1. 푸리에 급수, 푸리에 변환

A crazy idea of Fourier

Any periodic function can be rewritten as a weighted sum of sines and cosines of different frequencies.

모든 주기 함수는 무한개의 삼각함수의 선형결합 (weighted sum of sinusoids) 으로 표현할 수 있으며, 이를 푸리에 급수라고 한다.

그렇다면 비주기 함수는?

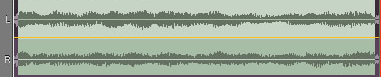
주기가 무한대인 주기함수로 보고 푸리에 급수를 활용할 수 있다, 이것이 푸리에 변환이다.

2. 푸리에 변환

푸리에 변환이란, 시간축 x 에서 존재하는 신호 혹은 정보를 주파수축 $\omega$ 으로 옮겨오겠다는 것이다.

푸리에 변환 (FT) 과 푸리에 역변환 (IFT) 는 다음 식과 같다.

$F(\omega)=\displaystyle\int_{-\infty}^{\infty}f(x)exp(-i\omega x)dx \; \Leftrightarrow \; f(x) = \frac{1}{2\pi}\displaystyle\int_{-\infty}^{\infty}F(\omega)exp(i\omega x)dx $

푸리에 급수에서 푸리에 변환 증명은 생략
* (Trigonometric Form) 모든 주기함수를 삼각함수들의 가중합으로 나타낼 수 있다.
* (Compact Form) sin 함수는 간단히 cos 함수로 변환할 수 있으니 cos 함수만의 합으로 나타낼 수도 있다.
* (Exponential Form) 삼각함수는 즉 지수함수이니, 지수함수들의 합으로 나타낼 수 있다. (오일러 방정식)

그렇다면, 푸리에 변환은 왜 할까?
(1) 데이터의 압축,   (2) spectral anaylsis

주파수차원으로 바꾸면 왜 데이터가 압축되고, spectral analysis가 가능할까?
이는 다음 그림을 통해 직관적으로 알 수 있다.

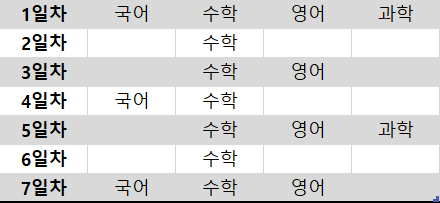원래 데이터

FT 데이터

저장할 정보의 양이 줄어들었을 뿐만 아니라, 이해(분석)하기도 쉽다.

3. Convolution과 Multiplication

시간 차원에서의 convolution 연산은, 주파수 차원에서의 multiplication 과 같다. 반대도 마찬가지.

즉, 차원이 바뀌면서 convolution 연산은 multiplication 연산으로 바뀌고, multiplication은 convolution 으로 바뀐다.

4. 위상과 크기의 의미

각 삼각함수의 magnitude(크기)와 phase(위상)은 복소수로 표현할 수 있다.

(1) 1-D 푸리에 변환
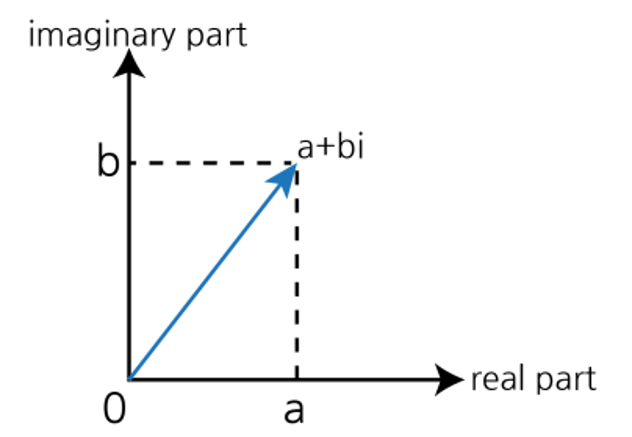1D Furier Transform

$a+b\;i$ 일때
$magnitude=\sqrt{a^2+b^2}$     : length of the complex number
$phase=\tan^{-1}(\frac{b}{a})$     : angle of complex number vector

(2) 2-D 푸리에 변환
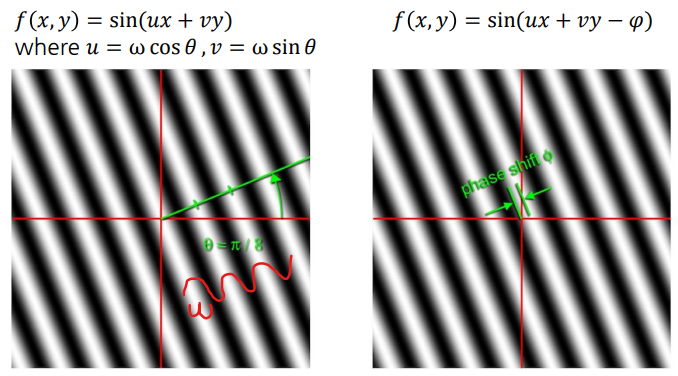2D Furier Transform

Angular frequency($\omega$)를 cos $\theta$, sin $\theta$ 를 곱하여 각각 $u$(x 방향에서의 angular frequency), $v$(y 방향에서의 angular frequency)

5. Low-pass, High-pass filter 의 의미

아래는 원본 이미지이다. Low-pass와 High-pass 필터를 통과시킬 때 FT 이미지는 다음과 같다.

Original image

(1) Low-Pass Filtering
Low-pass filtering
Low-pass image
주파수가 낮은 시그널만 통과(pass)시키고 높은 주파수는 제거하는 필터로, 가우시안 필터가 이에 해당한다.

(2) High-Pass Filtering
High-pass filtering
High-pass image
주파수가 높은 시그널만 통과시키는 필터로, edge (이미지 픽셀값이 급격히 변하는 부분) enhancer 가 이에 해당한다.

참고 문서

(1) Fourier Transform(푸리에 변환)의 이해와 활용_다크 프로그래머
(2) 푸리에 급수와 푸리에 변환(Fourier Transform)에 대해_린레몬 티스토리
(3) 정현파의 기초_공돌이의 수학정리노트