[KT AIVLE 4기] EDA

EDA (Explorary Data Analysis)

EDA란?

빅데이터에서 의미 있는 패턴을 찾고, 의사 결정에 필요한 인사이트를 얻기 위해서 데이터 분석이 수행된다.

혹은 AI 모델을 구축하기 전 타겟 특성을 예측하는데 도움이 될만한 입력 특성을 고르기 위해서 데이터 분석을 수행해야 한다.

데이터 분석은 크게 두 가지의 접근 방법이 있다. (1) EDA와 (2) CDA(confirmatory Data Analysis) 이다.

CDA가 추론 통계라면, EDA는 기술 통계에 해당한다고 볼 수 있다.

데이터 분석	프로세스	통계 기법
EDA	데이터 수집 > 시각화 탐색 > 패턴 도출 > 인사이트 발견	기술 통계 (모집단의 특성을 요약)
CDA	가설 설정 > 데이터 수집 > 통계 분석 > 가설 검증	추론 통계 (표본집단을 통해 모집단의 특성을 추론)

EDA를 통해 얻은 인사이트는 CDA의 가설로 설정될 수 있으며, 이를 검증하는 척도는 p.value(유의 확률)이다.

EDA 과정

1. 데이터 이해 및 전처리 (결측치, 이상치 확인)

2. 단변량 분석 (기초통계량 및 분포 확인)

3. 이변량 분석 (상관관계 확인)

---

1. 데이터 이해 및 전처리

데이터가 많다며, 앞부분 혹은 뒷부분만 보면 안 되므로, 무작위로 표본을 추출해서 관찰해봐야 한다.

단변량 분석과 함께 데이터를 이해할 수 있는데,

• 데이터의 중심을 알기 위해 : 평균, 중앙값, 최빈값

• 데이터의 분산도를 알기 위해 : 범위, 분산

• 데이터의 분포도를 알기 위해 : 왜도(skew), 첨도(kurosis) 를 사용할 수 있다.

(참고로, 평균은 이상치값에 영향을 많이 받으며 중앙값은 이상치의 존재에도 대표성이 있는 결과를 얻을 수 있다.)

---

2. 단변량 분석

기초통계량을 표와 그래프로 시각화한다.

숫자형 변수

기초통계량은 describe( ) 를 통해 구한다.

def eda_1_num(data, var, bins = 30):

    # 기초통계량
    print('<< 기초통계량 >>')
    display(data[[var]].describe().T)
    print('=' * 100)

    # 시각화
    print('<< 그래프 >>')
    plt.figure(figsize = (10,6))

    plt.subplot(2,1,1)
    sns.histplot(data[var], bins = bins, kde = True)
    plt.grid()

    plt.subplot(2,1,2)
    sns.boxplot(x = data[var])
    plt.grid()
    plt.show()

결과

var = 'Income'
eda_1_num(data, var)

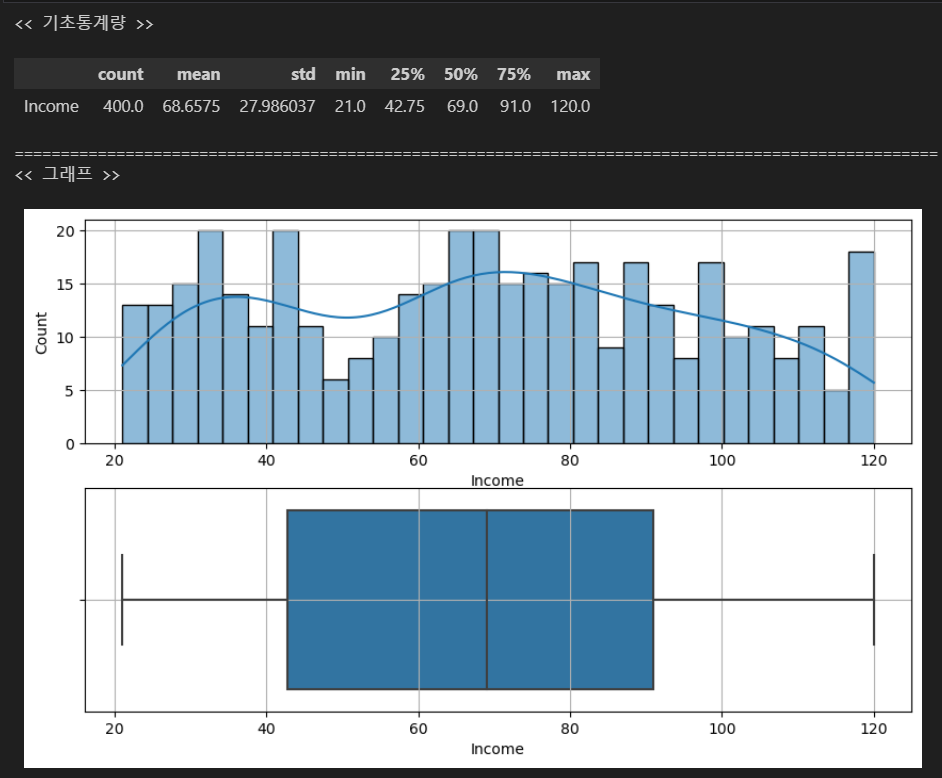
범주형 변수

기초통계량은 value_counts( ) 를 통해 구한다.

def eda_1_cat(data, var) :
    t1 = data[var].value_counts()
    t2 = data[var].value_counts(normalize = True)
    t3 = pd.concat([t1, t2], axis = 1)
    t3.columns = ['count','ratio']
    display(t3)
    
    sns.countplot(x = var, data = data)
    plt.show()

결과

var = 'ShelveLoc'
eda_1_cat(data, var)

---

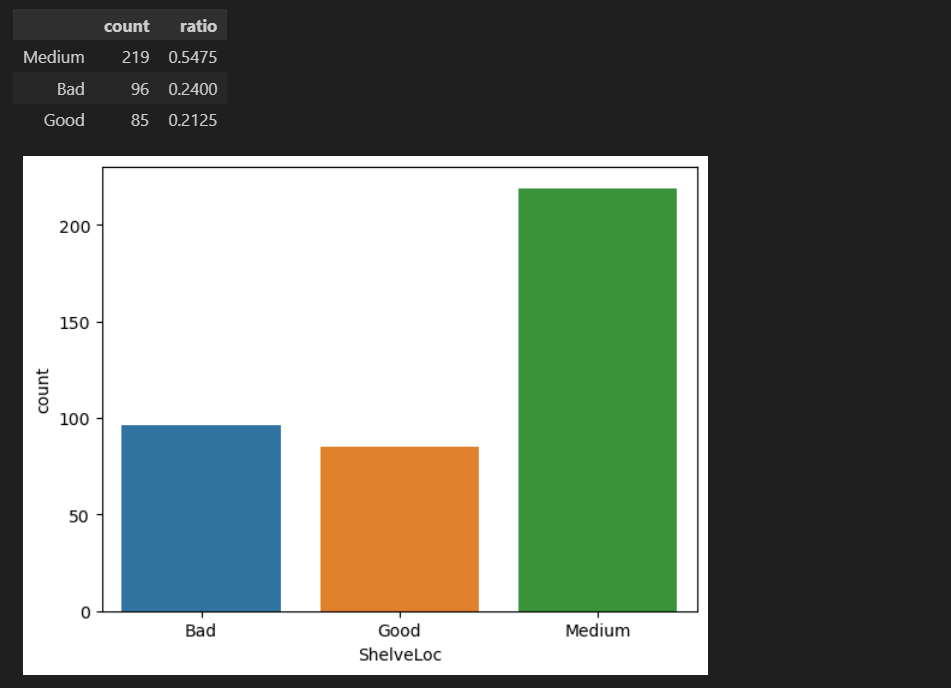
3. 이변량 분석

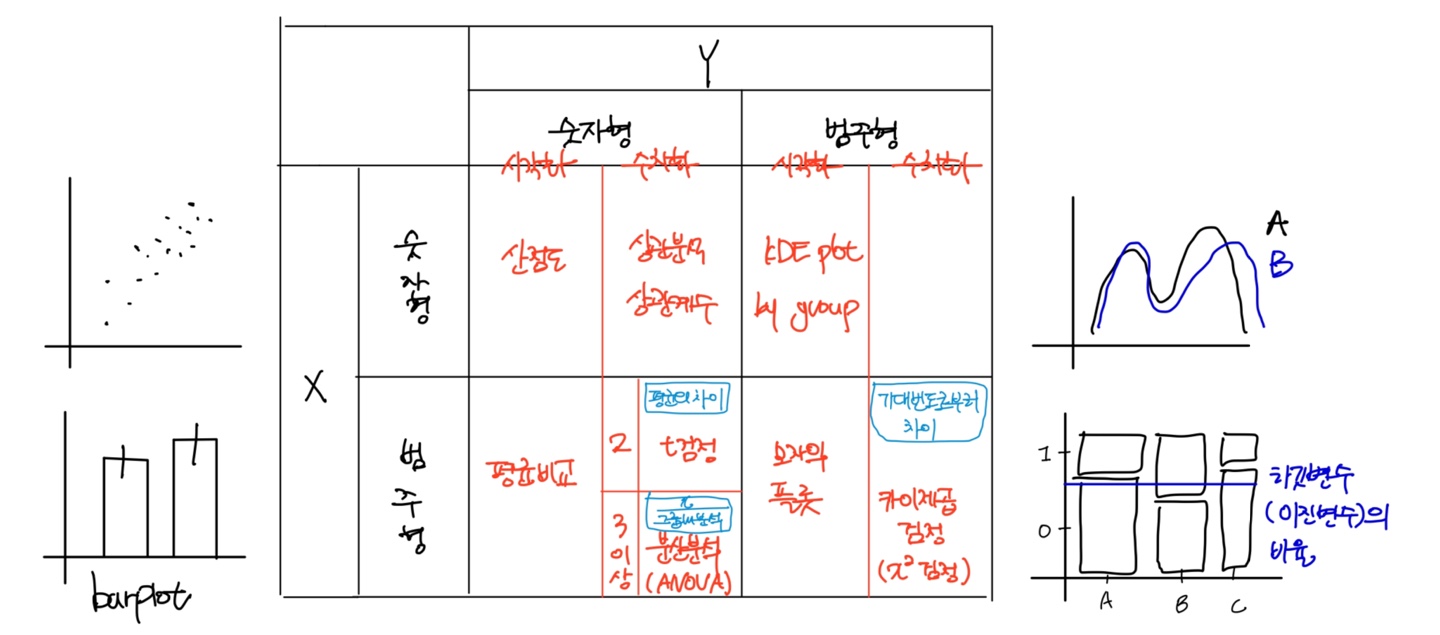
숫자형 -> 숫자형

def analyze(var, target, data=data):
    sns.scatterplot(x=var, y = target, data = data)
    plt.show()

    # sns.regplot(x=var, y = target, data = data)
    # plt.show()

    result = spst.pearsonr(data[var], data[target])
    print(f'상관계수 : {result[0]}, p-value : {result[1]}')

결과

analyze('Population', 'Sales')

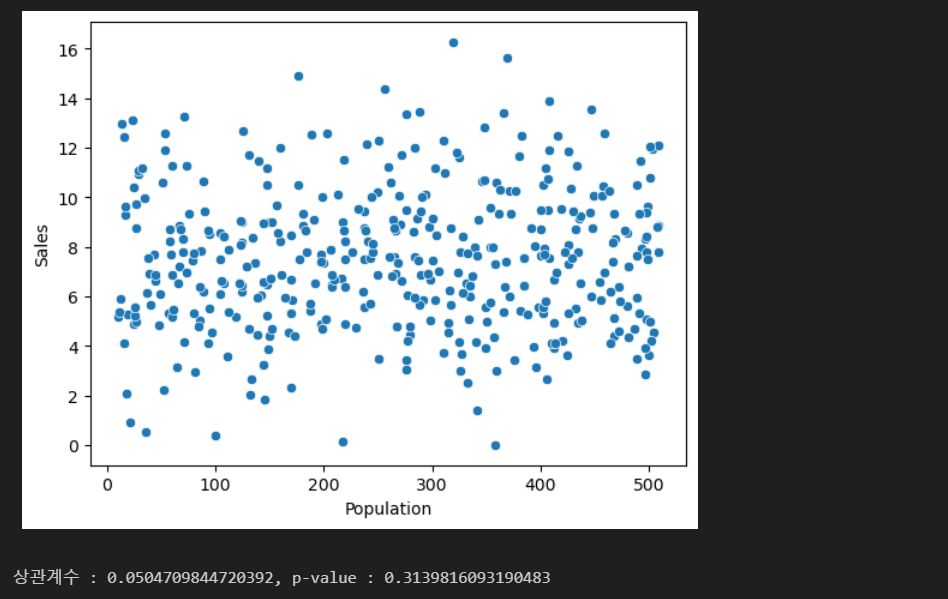
상관계수 > 0.5 이면 강한 상관관계

p-value(유의확률) < 0.05이면 상관계수가 의미가 있음을 의미

상관계수의 한계

• 비선형 관계를 잡지 못함

• 직선의 기울기 파악을 못함

=> 따라서, 산점도를 함께 봐야함

계단식 구조의 산점도

구간 안에서 상관관계가 성립하지 않음. 이럴 때는 숫자를 범주로 바꿔서 분석할 수 있다. (pd.cut)

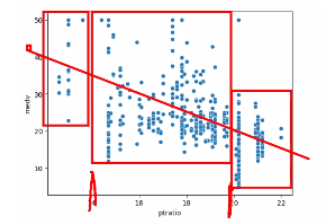
범주형 -> 숫자형

def analyze(var, target, data=data):
    sns.barplot(x = var, y = target, data=data)
    plt.show()
    
    temp = data.loc[data[var].notnull()]
    cate = data[var].unique()
    arg = []
    for i in cate:
        arg.append(temp.loc[temp[var] == i, target])
        
    ## t-test
    if len(cate) == 2:
        result =spst.ttest_ind(arg[0], arg[1])
        print(f't-통계량 : {result[0]}, p-value : {result[1]}')
    
    ## ANOVA
    else:
        result = spst.f_oneway(*arg)
        print(f'f-통계량 : {result[0]}, p-value : {result[1]}')

결과

analyze('Urban', 'Sales')

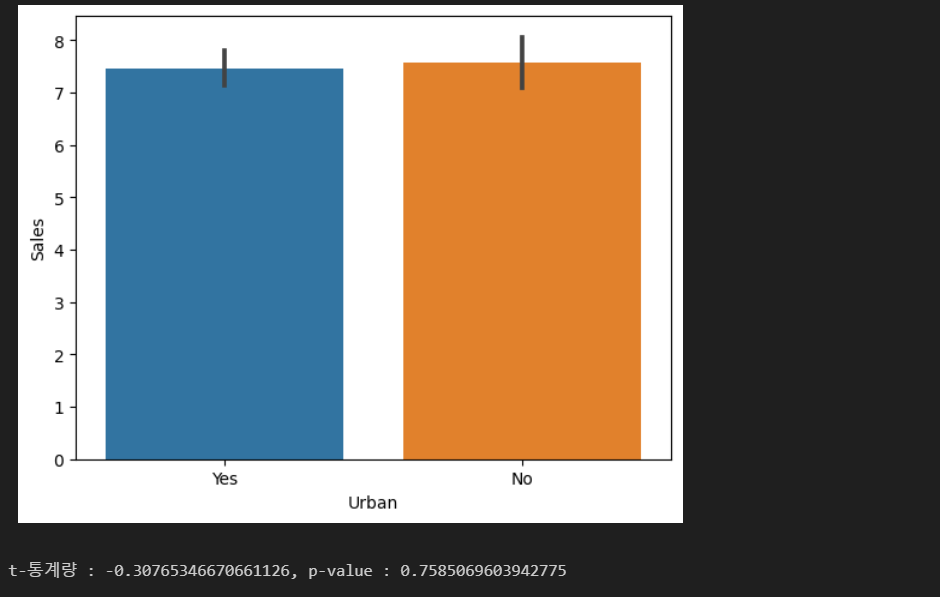
t-통계량, f-톻계량

t-통계량은 두 변수의 평균 간의 차이를 표준 오차로 나눈 값임.

\[t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]

• ( $\bar{x}_1$ )와 ( $\bar{x}_2$ ): 두 표본의 평균
• ( $s_1$ )와 ( $s_2$ ): 두 표본의 표준편차
• ( $n_1$ )와 ( $n_2$ ): 두 표본의 크기

t-통계량 > |2| 이면, 차이가 있음을 의미

f-통계량은 그룹 간의 분산과 그룹 내의 분산의 비율로 계산한 값임.

이는 분산 분석(ANOVA, ANalysis Of Variance)에서 주로 사용되며, 두 개 이상의 그룹 간의 평균 차이가 통계적으로 유의미한지를 검정하는 데 사용함.

\[F = \frac{\text{MSB (그룹 간의 분산)}}{\text{MSW (그룹 내의 분산)}} = \frac{\text{전체 평균 - 각 집단 평균}}{\text{각 집단의 평균 - 개별값}}\]

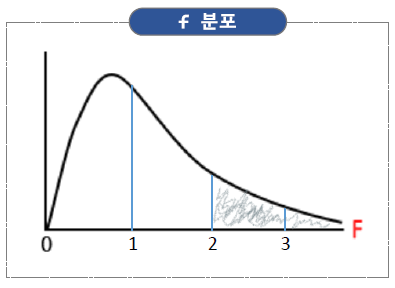
f-통계량 >= 2 이면, 차이가 있음을 의미

p-value(유의확률) < 0.05이면 t-통계량, f-통계량이 의미가 있음을 의미

숫자형 -> 범주형

feature = 'Age'

sns.kdeplot(x= feature, data = data, hue = target,
            common_norm = False)
plt.show()

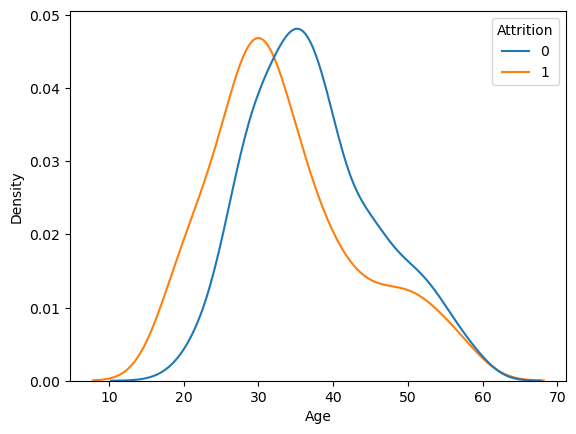
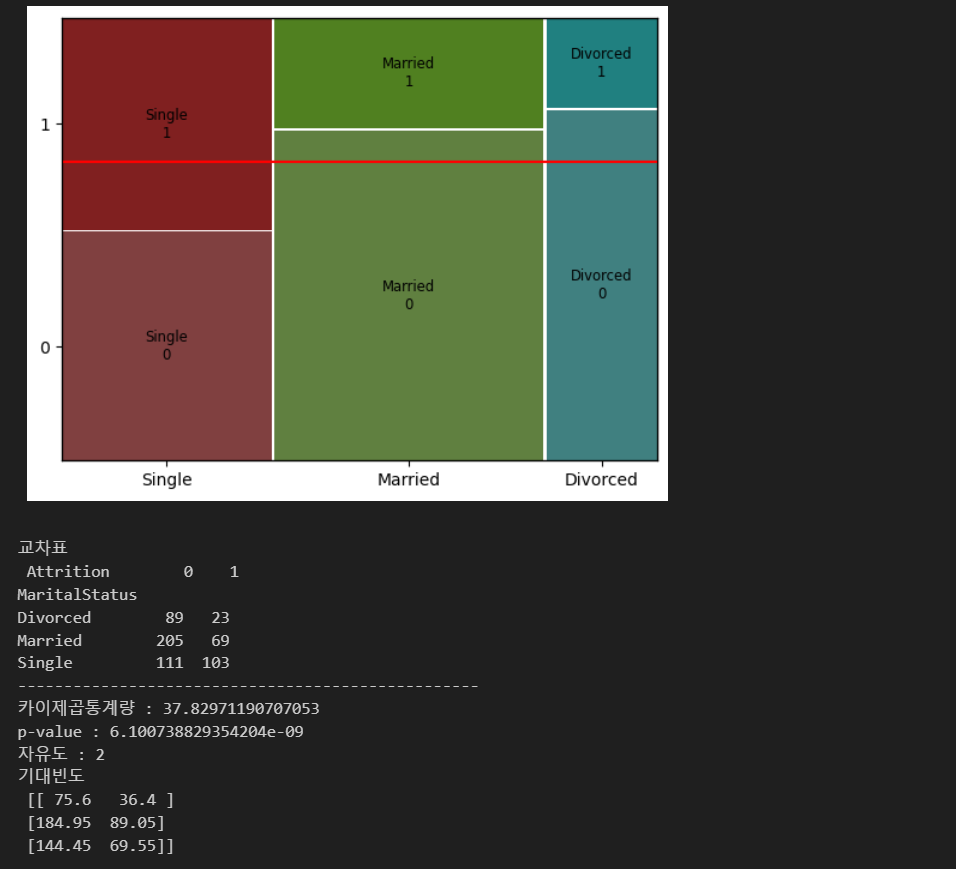
범주형 -> 범주형

def analyze(var,targ, data=data):
    mosaic(data, [var,target])
    plt.axhline(1-data[target].mean(), color='r')
    plt.show()
    
    table = pd.crosstab(data[var], data[targ])
    print(f'교차표\n {table}')
    print('-'*50)
    
    result = spst.chi2_contingency(table)
    print(f'카이제곱통계량 : {result[0]}')
    print(f'p-value : {result[1]}')
    print(f'자유도 : {result[2]}')
    print(f'기대빈도\n {result[3]}')

결과

analyze('MaritalStatus', 'Attrition')

카이제곱 통계량 (x2 통계량)

독립변수와 종속변수가 관련이 없다고 가정할 경우 기대되는 빈도와 실제 데이터의 차이를 계산한 값임.

두 범주형 변수 간의 독립성을 검정하는 데 사용함.

\[\chi^2 = \sum \frac{(O - E)^2}{E}\]

여기서:

• ( O ): 관측된 빈도
• ( E ): 기대된 빈도

카이제곱 통계량은 자유도(ν)의 2배보다 크면 차이가 있다고 봄.

자유도(ν)는 ( x 변수 범주의 수 -1 ) X ( y 변수 범주의 수 -1 ) 임.